Kirchhoffin piirilait
Kirchhoffin piirilait ovat sähködynamiikan peruslakeja yhdessä Ohmin lain kanssa. Kirchhoffin lakeja on kaksi: Kirchhoffin virtalaki ja Kirchhoffin jännitelaki.[1][2] Kirchhoffin lait kertovat, miten sähkövarauksen ja energian säilymislakeja voidaan soveltaa virtapiirien suunnitteluun. Kirchhoffin ja Ohmin lakien perusteella voidaan periaatteessa ratkaista jokainen virtapiirejä koskeva tehtävä.[1][3]
Preussilainen fyysikko Gustav Kirchhoff esitteli virtapiirejä koskevat lauseet vuonna 1845.[4] Hän esitti ensimmäisenä tavan analysoida sähköisiä virtapiirejä käyttäen solmupisteitä ja virtasilmukoita sellaisissa monimutkaisissa tilanteissa, joissa Ohmin laki ei riitä.[5] Kirchhoffin piirilakeja on kaksi: virta- ja jännitelaki. Kummatkin niistä pätevät sekä vaihto- että tasavirtapiireille.[3]
Kirchhoffin virtalaki[muokkaa | muokkaa wikitekstiä]

Kirchhoffin virtalakia kutsutaan myös nimellä Kirchhoffin ensimmäinen laki. Kirchhoffin virtalain mukaan sähkövirtaa ei tule mihinkään pisteeseen enempää kuin sieltä poistuu. Virtapiirin johtimet muodostavat verkon, jonka haarat liittyvät toisiinsa haaroitus- eli solmupisteissä. Näin ollen Kirchhoffin virtalain mukaan sähkövirtaa ei häviä eikä synny johtimien risteyskohdissa.[5][6]
Täten missä tahansa sähköjohtimien liitoskohdassa toteutuu:
Eli solmupisteeseen tulevien ja siitä poistuvien virtojen erotus on nolla.[7][5][8]
Kirchhoffin jännitelaki[muokkaa | muokkaa wikitekstiä]
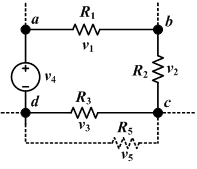
Kirchhoffin jännitelaki tunnetaan myös nimellä Kirchhoffin toinen laki.[6] Jännitelaki perustuu energian säilymislakiin. Sähkövarauksen jännitelähteestä saama potentiaalienergia kuluu sähkövirran kulkuun kaikkien virtapiirin vastusten läpi.[5] Tästä seuraa, että kuljettaessa täysi kierros virtapiirin ympäri potentiaalierojen summan pitää olla nolla.[3]
Kirchhoffin jännitelain mukaan jokaiselle suljetulle silmukalle on toteuduttava:
Eli suljetussa virtapiirissä lähdejännite on yhtä suuri kuin jännitehäviöiden summa.[7][6][8]
Laskentamenetelmä[muokkaa | muokkaa wikitekstiä]
Kirchhoffin piirilakeihin perustuu laskentamenetelmä, jolla voidaan ratkaista monimutkaisempienkin virtapiirien virtoja sekä myös impedansseja. Menetelmässä hyödynnetään sekä Kirchhoffin virta- että jännitelakia.
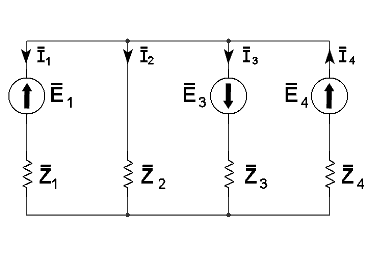
- Menetelmän ensimmäisessä vaiheessa merkitään jokaiseen virtapiirin haaraan virta ja sen arvioitu kulkusuunta.
- Lasketaan piirin solmupisteiden lukumäärä n.
- Kirjoitetaan n-1 virtalain mukaista yhtälöä, yhtälöt saa kirjoittaa haluamiinsa virtapiirin solmupisteisiin.
- Loput yhtälöistä kaikkien tuntemattomien ratkaisemiseksi kirjoitetaan jännitelain avulla.
- Jänniteyhtälöt saa kirjoittaa mille tahansa reitille, kunhan jokaisen virtapiirin haaran kautta kuljetaan kerran.
Laskuesimerkki[muokkaa | muokkaa wikitekstiä]
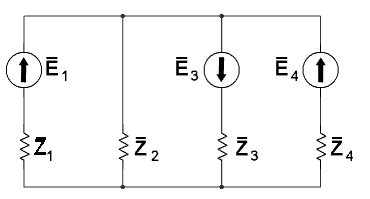
Esimerkissä on esitetty vaihtovirtapiiri, mutta menetelmä pätee myös tasavirtapiireissä.
- Lasketaan solmupisteiden lukumäärä n(2).
- Kirjoitetaan n-1 virtalain mukaista yhtälöä.
- Kirjoitetaan tarvittava määrä jännitelain mukaisia yhtälöitä (3 silmukkaa, kiertäen myötäpäivään).
- Nyt voidaan ratkaista virrat
Muita virtapiirien laskentamenetelmiä[muokkaa | muokkaa wikitekstiä]
- Tähtipistepotentiaalimenetelmä
- Nortonin menetelmä
- Theveninin menetelmä
- Silmukkamenetelmä
- Solmumenetelmä
Katso myös[muokkaa | muokkaa wikitekstiä]
Lähteet[muokkaa | muokkaa wikitekstiä]
- ↑ a b Aura, Lauri & Tonteri, Antti J.: Teoreettinen sähkötekniikka ja sähkökoneiden perusteet. porvoo: WSOY, 1994. ISBN 951-0-21385-3.
- ↑ Kimmo Silvonen: Sähkötekniikka ja piiriteoria, s. 16 ja 20. Helsinki: Otatieto, 2009. ISBN 978-951-672-362-7.
- ↑ a b c Grant, I. S. & Phillips, W. R.: ”8.1.1”, Electromagnetism, 2. painos, s. 283. Wiley, 2003. ISBN 0-471-92712-0. (englanniksi)
- ↑ Lindell, Ismo: Sähkön pitkä historia, s. 154–155. "Piiritekniikan kehitystä". Helsinki: Otatieto, 2009. ISBN 978-951-672-358-0.
- ↑ a b c d Inkinen, Pentti & Manninen, Reijo & Tuohi, Jukka: Momentti 2 – Insinöörifysiikka. Helsinki: Otava, 2003. ISBN 951-1-18457-1.
- ↑ a b c Ruppa, Erkki & Lilja, Tuomi: Sähkötekniikkaa sivuaineopiskelijoille. Helsinki: Opetushallistus, 1994. ISBN 951-719-777-2.
- ↑ a b Young & Freedman: ”26.2”, University Physics with Modern Physics, 11. painos, s. 986–987. Pearson, 2004. ISBN 0-321-20469-7. (englanniksi)
- ↑ a b Mäkelä, Mikko & Soininen, Lauri & Tuomola, Seppo & Öistämö, Juhani: Tekniikan kaavasto. Jyväskylä: Tammertekniikka, 2002. ISBN 951-9004-74-2.
Kirjallisuutta[muokkaa | muokkaa wikitekstiä]
- Voipio, Erkki: Virtapiirit ja verkot. Helsinki: Otatieto, 2001 (1976). ISBN 951-672-082-X.