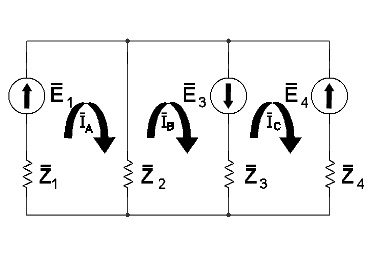Silmukkamenetelmä

Silmukkamenetelmä (myös silmukkavirtamenetelmä) on eräs sähköisten virtapiirien ja verkkojen ratkaisuun liittyvä systemaattinen menetelmä. Silmukkamenetelmässä käytetään Kirchhoffin jännitelakia ja tällöin saadaan selvitettyä virtapiirin silmukoissa kulkevat virrat.

• Nähdään virtapiiri moniruutuisena ikkunana ja merkitään joka ruutuun silmukkavirta ${\bar {I}}_{A},{\bar {I}}_{B}...{\bar {I}}_{n}$
• Joka ruudulle kirjoitetaan oma jänniteyhtälö ja ratkaistaan silmukoissa kulkevat virrat.
• Ruuduille yhteisten komponenttien resistanssi/impedanssi pitää huomioida molempien silmukkavirtojen osalta.
• Silmukkavirran kiertosuunnan saa valita vapaasti.

Laskuesimerkki

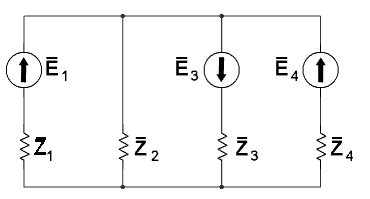
Selvitetään piirissä kulkevat silmukkavirrat sekä haaroissa kulkevat yksittäiset virrat.

• Esimerkissä oletetaan vaihtovirtalähteiden toimivan samalla taajuudella: eri nimellistaajuuksisille virtalähteille ei menetelmää voi suoraan soveltaa.
• Laskuesimerkki pätee myös tasavirtapiireille.

• Kirjoitetaan jokaiselle ruudulle oma jänniteyhtälö:

${\bar {E}}_{1}={\bar {I}}_{A}\cdot ({\bar {Z}}_{1}+{\bar {Z}}_{2})-{\bar {I}}_{B}\cdot {\bar {Z}}_{2}$

${\bar {E}}_{3}=-{\bar {I}}_{A}\cdot {\bar {Z}}_{2}+{\bar {I}}_{B}\cdot ({\bar {Z}}_{2}+{\bar {Z}}_{3})-{\bar {I}}_{C}\cdot {\bar {Z}}_{3}$

$-{\bar {E}}_{4}-{\bar {E}}_{3}=-{\bar {I}}_{B}\cdot {\bar {Z}}_{3}+{\bar {I}}_{C}\cdot ({\bar {Z}}_{3}+{\bar {Z}}_{4})$

• Nyt voidaan ratkaista silmukkavirrat ${\bar {I}}_{A}$, ${\bar {I}}_{B}$ ja ${\bar {I}}_{C}$
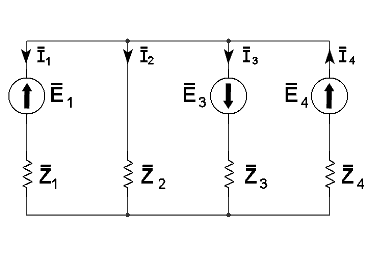
• Yksittäisten haarojen virrat voidaan laskea seuraavasti:

${\bar {I}}_{1}=-{\bar {I}}_{A}$

${\bar {I}}_{2}={\bar {I}}_{A}-{\bar {I}}_{B}$

${\bar {I}}_{3}={\bar {I}}_{B}-{\bar {I}}_{C}$

${\bar {I}}_{4}=-{\bar {I}}_{C}$

• Mikäli virran arvoksi tulee negatiivinen luku, tarkoittaa se sitä, että virran todellinen kulkusuunta on vastakkainen piiriin merkitylle.

Muita virtapiirien laskentamenetelmiä

• Nortonin menetelmä
• Theveninin menetelmä
• Kirchhoffin laskentamenetelmä
• Tähtipistepotentiaalimenetelmä
• Solmumenetelmä

Kirjallisuutta

• Voipio, Erkki: Virtapiirit ja verkot. Helsinki: Otatieto, 2001 (1976). ISBN 951-672-082-X.

Aiheesta muualla

• http://www.ct.tkk.fi/courses/ca1/PDF/color/week04.pdf TKK:n Piirianalyysin peruskurssin luentokalvot