Ekmanin spiraali

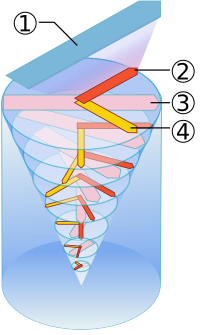
Ekmanin spiraali. Punaisella on merkitty yläpuolisen vesikerroksen virtaussuuntaa, keltaisella Coriolisvoimaa ja vaaleanpunaisella vesikerroksen todellista virtaussuuntaa.

Ekmanin spiraali viittaa virtausten tai tuulten rakenteeseen rajakerroksessa eli nesteen tai kaasun rajapinnan lähellä. Siinä virtauksen suunta muuttuu spiraalinomaisesti, kun liikutaan rajapinnasta poispäin. Ilmiö on nimetty ruotsalaisen oseanografin Vagn Walfrid Ekmanin mukaan. Pintavirtausten poikkeamat huomasi ensimmäisen kerran norjalainen oseanografi Fridtjof Nansen 1890-luvulla havaitessaan, että ajelehtiva vene kulki tuulen suunnasta oikealle.

Ekmanin spiraali on seurausta kitkasta ja Coriolis-ilmiöstä, joka kääntää pohjoisella pallonpuoliskolla virtauksia liikesuuntansa nähden oikealle ja eteläisellä vasemmalle. Kun siis tuuli puhaltaa valtameren pinnalle pohjoisella pallonpuoliskolla, pinnan virtaus kääntyy tuulen suunnasta noin 45 astetta oikealle (todellisuudessa vain 20–30 astetta). Kitkan vuoksi pintavesi saa myös alemmat vesikerrokset liikkeelle, ja alapuolella oleva vesi kääntyy aina yläpuolella olevaa enemmän oikealle. Pintavirtauksenkin nopeus on vain muutamia prosentteja tuulen nopeudesta, ja syvemmälle mentäessä virtauksen nopeus edelleen pienenee.

Klassinen Ekmanin spiraali on havaittu merijään alla, mutta sitä ei ole löydetty avomeriolosuhteissa. Tämä johtuu pinta-aaltojen häiritsevästä vaikutuksesta ja valtameren pintakerroksen turbulenttisesta sekoittumisesta. Jonkinasteista kiertymistä havaitaan usein. Ilmakehän rajakerroksessa Ekmanin spiraali on tyypillinen, ja sen voimakkuus riippuu stabiilisuudesta ja alustan rosoisuudesta.

Niin sanotulla Ekman-syvyydellä virtauksen suunta on kiertynyt 180 astetta eli virtaus on pintavirtauksen kanssa vastakkaissuuntainen. Tyypillinen Ekman-syvyys meressä on muutamia kymmeniä metrejä.

Spiraalin fysiikka

Ekmanin teorian tärkeimpänä oletuksena oli syvä, rannaton meri, joka on horisontaalisesti homogeeninen. Tällöin advektiota ei lähtökohtaisesti tapahdu eikä painegradienttia ole, jolloin veden virtausyhtälöt, ns. Navierin–Stokesin yhtälöt tiivistyvät x- ja y-suunnissa muotoon

${\frac {\partial u}{\partial t}}=fv+\nu {\frac {\partial ^{2}u}{\partial z^{2}}}\,$

${\frac {\partial v}{\partial t}}=-fu+\nu {\frac {\partial ^{2}u}{\partial z^{2}}}\,$

missä ${\vec {V}}=u{\hat {i}}+v{\hat {j}}$ on virtausnopeus, $f=2\Omega \sin \phi$ on Coriolis-parametri, $\nu$ veden kinemaattinen viskositeetti ja z syvyys.

Lisäksi Ekman oletti, että vallitseva etelätuuli kohdistaa +y-suuntaisen leikkausjännityksen $\tau$ veteen. Näistä lähtökohdista hän johti edelliselle yhtälöparille ratkaisun

$\left\{{\begin{matrix}u=V_{0}e^{-{\frac {\pi z}{D}}}\cos({\frac {\pi }{4}}-{\frac {\pi z}{D}})\\v=V_{0}e^{-{\frac {\pi z}{D}}}\sin({\frac {\pi }{4}}-{\frac {\pi z}{D}})\end{matrix}}\right.\,$

missä on merkitty V₀:lla tuulen ajovirran voimakkuutta, asetettu z > 0 sekä määritelty Ekman-syvyys (alun perin Depth of Wind-current)

$D=\pi {\sqrt {\frac {2\nu }{|f|}}}\,$

Koska virtausprofiiliin ja veden pystysuuntaiseen sekoittumiseen vaikuttavat muutkin tekijät kuin ne, jotka oletukseen sisältyvät (esimerkiksi stabiilisuus ja pyörteiden koko ja muoto), kirjoitetaan tavallisemmin $\nu$:n paikalle turbulenttinen viskositeetti, jonka suuruusluokka voi olla $A_{z}\sim 40{\text{ m}}^{2}{\text{ s}}^{-1}$.

Aiheesta muualla

• American Meteorological Societyn sanasto – matemaattinen kuvaus (englanniksi)