Ero sivun ”Graafi” versioiden välillä
| [katsottu versio] | [katsottu versio] |
Ei muokkausyhteenvetoa |
Ei muokkausyhteenvetoa |
||
| Rivi 4: | Rivi 4: | ||
:<math>G = (V, E)</math>, |
:<math>G = (V, E)</math>, |
||
jossa ''V'' on joukko solmuja eli pisteitä ({{k-en|vertex}}, monikko: ''vertices'') ja ''E'' joukko kaaria eli viivoja eli välejä (''edges''). Kaarijoukon määritelmä voi vaihdella, mutta yleisin tapaus on |
jossa ''V'' on joukko [[solmu (verkko)|solmuja]] eli pisteitä eli noodeja ({{k-en|vertex}}, monikko: ''vertices'', tai ''node'') ja ''E'' joukko kaaria eli viivoja eli välejä eli nuolia eli särmiä (''edges''). Kaarijoukon määritelmä voi vaihdella, mutta yleisin tapaus on |
||
:<math>E \subset \{(a, b) : a, b \in V\}</math> |
:<math>E \subset \{(a, b) : a, b \in V\}</math> |
||
jolloin kaarella voi olla suunta ja se voi yhdistää solmun itseensä. |
jolloin kaarella voi olla suunta ja se voi yhdistää solmun itseensä. Termiä "nuoli" ei käytetä, jos kaaret määritelläänkin vain kahden solmun joukoiksi eli niillä ei ole suuntaa. |
||
Graafina voidaan mallintaa monia ongelmia, jotka pystytään ratkaisemaan algoritmisesti tietojenkäsittelytieteen keinoin. |
Graafina voidaan mallintaa monia ongelmia, jotka pystytään ratkaisemaan algoritmisesti tietojenkäsittelytieteen keinoin. |
||
| Rivi 15: | Rivi 15: | ||
[[Tiedosto:Directed acyclic graph.png|right|thumb|Kuva suunnatusta graafista, jossa on 8 solmua ja 9 kaarta.]][[Tiedosto:Undirected graph.svg|right|thumb|Kuva suuntaamattomasta graafista, jossa on 4 solmua ja 4 kaarta.]] |
[[Tiedosto:Directed acyclic graph.png|right|thumb|Kuva suunnatusta graafista, jossa on 8 solmua ja 9 kaarta.]][[Tiedosto:Undirected graph.svg|right|thumb|Kuva suuntaamattomasta graafista, jossa on 4 solmua ja 4 kaarta.]] |
||
Graafeja voidaan jaotella eri luokkiin sen mukaan, mitä ominaisuuksia niillä on. Jos esimerkiksi |
Graafeja voidaan jaotella eri luokkiin sen mukaan, mitä ominaisuuksia niillä on. Jos esimerkiksi |
||
graafin jokaista solmuparia (a, b) yhdistävästä kaaresta seuraa aina, että myös solmujen (b, a) välillä on kaari, sanotaan, että graafi on ''suuntaamaton''. Vastaavasti jos mistä hyvänsä solmusta päästään mihin tahansa toiseen solmuun kulkemalla riittävän monen solmun ja kaaren kautta, graafi on ''kytketty''. Painotetussa graafissa jokaisella kaarella on kerroin. Jos jokaisesta solmusta pääsee jokaiseen toiseen solmuun vain yhtä reittiä, eli graafissa ei ole syklejä, sitä kutsutaan [[puu (graafiteoria)|puu]]ksi. |
graafin jokaista solmuparia (a, b) yhdistävästä kaaresta seuraa aina, että myös solmujen (b, a) välillä on kaari, sanotaan, että graafi on ''suuntaamaton''. Vastaavasti jos mistä hyvänsä solmusta päästään mihin tahansa toiseen solmuun kulkemalla riittävän monen solmun ja kaaren kautta, graafi on ''kytketty''. Painotetussa graafissa jokaisella kaarella on kerroin. |
||
=== Puu === |
|||
Jos jokaisesta solmusta pääsee jokaiseen toiseen solmuun vain yhtä reittiä, eli graafissa ei ole syklejä, sitä kutsutaan [[puu (graafiteoria)|puu]]ksi. |
|||
Puun kaaria kutsutaan myös oksiksi. Lehdiksi kutsutaan solmuja, joiden lähtöaste on nolla (eli jotka eivät ole minkään nuolen alkupisteitä).<ref>{{Verkkoviite| osoite=http://math.tut.fi/~ruohonen/GT.pdf | nimeke=GRAAFITEORIA | tekijä=Sovelletun matematiikan professori Keijo Ruohonen | ajankohta=2013}}</ref> |
|||
== Tietorakenne == |
== Tietorakenne == |
||
| Rivi 46: | Rivi 51: | ||
Ehkä tunnetuin NP-täydellisistä ongelmista on [[Kauppamatkustajan ongelma]], jossa on tavoitteena löytää lyhin mahdollinen reitti, joka kulkee kaikkien kauppamatkustajan listassa olevien kaupunkien kautta. Tietojenkäsittelytiede ei kuitenkaan ole varma siitä, ovatko NP-täydellisiksi luetellut ongelmat ratkaistavissa jollain menetelmällä polynomisessa ajassa. |
Ehkä tunnetuin NP-täydellisistä ongelmista on [[Kauppamatkustajan ongelma]], jossa on tavoitteena löytää lyhin mahdollinen reitti, joka kulkee kaikkien kauppamatkustajan listassa olevien kaupunkien kautta. Tietojenkäsittelytiede ei kuitenkaan ole varma siitä, ovatko NP-täydellisiksi luetellut ongelmat ratkaistavissa jollain menetelmällä polynomisessa ajassa. |
||
== Viitteet == |
|||
{{viitteet}} |
|||
== Lähteet == |
== Lähteet == |
||
Versio 25. lokakuuta 2019 kello 18.42
Graafi eli verkko on matematiikkaan (graafiteoria eli verkkoteoria) ja tietojenkäsittelytieteeseen liittyvä käsite. Se koostuu joukosta solmuja ja joukosta niitä yhteen liittäviä kaaria. Matemaattisesti ilmaistuna graafi eli verkko G on järjestetty pari
- ,
jossa V on joukko solmuja eli pisteitä eli noodeja (engl. vertex, monikko: vertices, tai node) ja E joukko kaaria eli viivoja eli välejä eli nuolia eli särmiä (edges). Kaarijoukon määritelmä voi vaihdella, mutta yleisin tapaus on
jolloin kaarella voi olla suunta ja se voi yhdistää solmun itseensä. Termiä "nuoli" ei käytetä, jos kaaret määritelläänkin vain kahden solmun joukoiksi eli niillä ei ole suuntaa.
Graafina voidaan mallintaa monia ongelmia, jotka pystytään ratkaisemaan algoritmisesti tietojenkäsittelytieteen keinoin.
Luokittelu
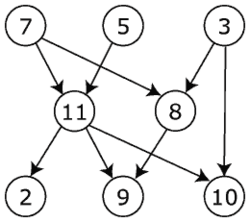

Graafeja voidaan jaotella eri luokkiin sen mukaan, mitä ominaisuuksia niillä on. Jos esimerkiksi graafin jokaista solmuparia (a, b) yhdistävästä kaaresta seuraa aina, että myös solmujen (b, a) välillä on kaari, sanotaan, että graafi on suuntaamaton. Vastaavasti jos mistä hyvänsä solmusta päästään mihin tahansa toiseen solmuun kulkemalla riittävän monen solmun ja kaaren kautta, graafi on kytketty. Painotetussa graafissa jokaisella kaarella on kerroin.
Puu
Jos jokaisesta solmusta pääsee jokaiseen toiseen solmuun vain yhtä reittiä, eli graafissa ei ole syklejä, sitä kutsutaan puuksi.
Puun kaaria kutsutaan myös oksiksi. Lehdiksi kutsutaan solmuja, joiden lähtöaste on nolla (eli jotka eivät ole minkään nuolen alkupisteitä).[1]
Tietorakenne
Tietojenkäsittelytieteessä graafia käytetään myös abstraktina tietotyyppinä tai tietorakenteena. Se toteutetaan yleensä vieruslistoina tai vierusmatriisina. Vieruslistaesityksessä solmun naapurit säilötään linkitettyyn listaan. Vierusmatriisiesityksessä matriisin alkion (a, b) arvo on tosi, jos solmusta a pääsee solmuun b, muuten epätosi.
Aina graafia ei tarvitse toteuttaa konkreettisena tietorakenteena. Solmun perusteella voidaan generoida lennossa uusia solmuja. Rekursiiviset funktioiden kutsut saattavat muodostaa verkkomaisen rakenteen. Joskus solmuista tiedetään ennalta jotain: esimerkiksi ruudukon ruudulla (x, y) on aina kahdeksan naapuria: (x + 1, y), (x, y + 1), (x + 1, y + 1) ja niin edelleen.
Sovellusalueita
Graafeja ja niihin liittyviä algoritmeja käytetään varsin monissa erilaisissa sovellutuksissa. Esimerkkeinä mainittakoon vaikkapa lyhimmän tai ylipäätään reitin etsiminen ja riippuvuussuhteiden esittäminen sopivassa järjestyksessä (ks. topologinen lajittelu). Ylipäätään minkä hyvänsä ongelman ratkaisu, missä tiedetään alkutila, sallitut seuraajatilat ja tavoitetila (mutta ei suoraan miten sinne päästään), voidaan ainakin periaatteessa tuottaa graafialgoritmeilla.
Esimerkkejä
Graafeja voidaan mallintaa monin eri tavoin. Ohessa esimerkki suuntaamattomasta graafista, joka kuvaa VR:n rataverkkoa muutaman suuremman kaupungin osalta:
G = (("Tampere", "Turku"), ("Tampere", "Jyväskylä"), ("Tampere", "Helsinki"), ("Helsinki", Turku"), ("Tampere", "Oulu"))
Yllä oleva graafi voitaisiin esittää visuaalisesti vaikkapa näin:
Graafista näkee esimerkiksi sen, että Helsingistä pääsee suoraan Turkuun, mutta että Jyväskylästä ja Oulusta pitää mennä aina Turkuun Tampereen kautta.
Graafeihin liittyviä ongelmia
Graafeihin liittyy monia suuria avoimia ongelmia, joiden ratkaiseminen toisi keksijälle mainetta ja kunniaa. Monet graafeissa esiintyvistä ongelmista luokitellaan tietojenkäsittelytieteessä NP-täydellisiksi. Se tarkoittaa lyhyesti sanottuna sitä, että kyseinen ongelma on nykyisten tietokoneiden laskentakapasiteetin ulkopuolella, jos graafin solmujen tai kaarien joukko kasvaa riittävän isoksi. Emme siis tiedä menetelmää, jolla kyseinen ongelma voidaan ratkaista järkevässä ajassa.
Ehkä tunnetuin NP-täydellisistä ongelmista on Kauppamatkustajan ongelma, jossa on tavoitteena löytää lyhin mahdollinen reitti, joka kulkee kaikkien kauppamatkustajan listassa olevien kaupunkien kautta. Tietojenkäsittelytiede ei kuitenkaan ole varma siitä, ovatko NP-täydellisiksi luetellut ongelmat ratkaistavissa jollain menetelmällä polynomisessa ajassa.
Viitteet
- ↑ Sovelletun matematiikan professori Keijo Ruohonen: GRAAFITEORIA math.tut.fi. 2013.
Lähteet
- Thomas Cormen & Charles Leiserson & Ronald Rivest & Clifford Stein: Introduction to Algorithms – 2nd ed., s. 524–531. MIT Press ja McGraw-Hill, 2001. ISBN 0-262-03293-7.
Kirjallisuutta
- Ruohonen, Keijo: Graafiteoria. Opintomoniste 136. Tampere: TTKK, 1990. ISBN 951-721-530-4.


