Horisontti

Horisontti eli taivaanranta on näennäinen viiva, joka erottaa toisistaan maan ja taivaan jakaen näkökentän kaikki suunnat kahteen osaan: niihin, jotka kohtaavat Maan pinnan, ja niihin, jotka eivät kohtaa. Monissa paikoissa todellinen horisontti ei ole näkyvissä, sillä sen peittävät esimerkiksi puut, rakennukset tai vuoret, ja näiden vaikutuksesta taivaasta näkyy pienempi osa, jonka rajaa sanotaan näkyväksi horisontiksi.
Sana horisontti on peräisin kreikan kielen sanoista "ὁρίζων κύκλος" (horizōn kyklos), "rajoittava ympyrä"[1][2],
Merkitys[muokkaa | muokkaa wikitekstiä]

Historiallisesti näköetäisyys merellä on ollut erittäin tärkeä, sillä ennen radion ja lennättimen kehitystä se oli suurin etäisyys, jolle voitiin lähettää sanomia ilman välikäsiä.
Monissa yhteyksissä, erityisesti perspektiivipiirustuksessa, Maan pinnan kaarevuutta ei oteta huomioon, ja horisontiksi käsitetään teoreettinen linja, jolla kaikkien vaakasuorien tasojen vastineet kohtaavat, kun ne projisoidaan kuvapinnalle ja etäisyys pinnalla olevaan kuvattavaan kohteeseen kasvaa rajatta. Tämä geometrinen horisontti määritellään siis olettamalla, että havaitsija olisi äärettömällä tasaisella pinnalla. Lähellä merenpintaa olevan havaitsijan geometrinen horisontti on niin lähellä todellista horisonttia, että eroa ei paljain silmin näe, mutta katsottaessa tuhannen metrin korkuiselta vuorelta merta todellinen horisontti on noin asteen verran geometrisen horisontin eli katsojan silmien kautta kulkevan vaakatason alapuolella.
Pallotähtitieteessä horisontilla tarkoitetaan havaitsijan silmien kautta kulkevaa vaakasuoraa tasoa, tai sen ja taivaanpallon leikkausviivaa. Se on horisonttijärjestelmässä korkeuden perustaso, jonka muodostavat ne pisteet, joiden korkeuskulma on nolla.[3] Tämä määritellään siis samaan tapaan kuin geometrinen horisontti.
Horisontin etäisyys[muokkaa | muokkaa wikitekstiä]
Suurin etäisyys, jolle tasaisella maalla tai merellä lähellä maan pintaa oleva havaitsija voi nähdä, voidaan likimäärin laskea kaavalla [4]
missä d on etäisyys kilometreinä ja h havaitsijan silmien korkeus metreinä.
Esimerkkejä:
- Maan pinnalla havaitsija, jonka silmät ovat 1,70 metrin korkeudella, näkee tasaisella maalla noin 5 kilometrin päähän.
- Sadan metrin korkuisella vuorella tai tornissa oleva havaitsija näkee muutoin tasaisella maalla tai meren rannalla 39 kilometrin päähän.
- Maailman korkeimman rakennuksen, Burj Khalifan ylimmästä kerroksesta, 828 metrin korkeudesta, näkee 111 kilometrin päähän.
Tässä kaavassa on otettu huomioon ilmakehässä tapahtuvan valon taittumisen vaikutus.
Geometrinen malli[muokkaa | muokkaa wikitekstiä]


Jos oletetaan Maan olevan täydellinen pallo, jonka ilmakehä ei vaikuta havaintoon, horisontin etäisyys eli suurin näköetäisyys voidaan helposti laskea euklidisen geometrian avulla.
Olkoon O ympyrän ulkopuolella oleva piste. Piirretään tämän pisteen kautta kulkeva ympyrän tangentti, joka sivuaa ympyrää pisteessä C, sekä pisteen O ja ympyrän keskipisteen kautta kulkeva sekantti, joka leikkaa ympyrän pisteissä A ja B. Tällöin on sekanttilauseen mukaan
- .
Jos ympyrä esittää maapalloa ja piste O havaitsijan silmää ja käytetään etäisyyksille seuraavia merkintöjä:
- d = OC = horisontin etäisyys
- D = AB = Maan halkaisija
- h = OB = havaitsijan korkeus merenpinnasta mitattuna
- D+h = OA = Maan halkaisijan ja havaitsijan korkeuden summa,
kaava saadaan muotoon
tai
missä R on Maan säde.
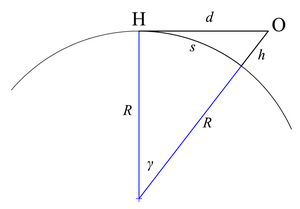
Vaihtoehtoisesti yhtälö voidaan johtaa Pythagoraan lauseen avulla. Koska näköviiva on Maan pinnan tangentti, se on horisontissa kohtisuorassa Maan sädettä vastaan. Täten muodostuu suorakulmainen kolmio, jonka hypotenuusan pituus on Maan säteen ja havaitsijan korkeuden summa. Jos käytetään merkintöjä
- d = etäisyys horisonttiin
- h = havaitsijan korkeus meren pinnan tasosta mitattuna
- R = Maan säde,
saadaan :
Mikäli etäisyys horisonttiin (s) mitataan Maan kaarevaa pintaa pitkin ja kulma γ ilmoitetaan radiaaneina, saadaan
joten
Tästä s saadaan ratkaistuksi:
Tämä etäisyys s voidaan ilmoittaa myös näköviivan d pituuden avulla; oikealla olevasta kuvasta,
Jos tässä γ korvataan etäisyydellä s ja ratkaistaan yhtälö s:n suhteen, saadaan edelleen
Jos havaitsijan korkeus h on paljon pienempi kuin Maan säde R, ovat suora etäisyys havaitsijan silmästä horisonttiin (d) ja etäisyys Maan pintaa pitkin (s) käytännöllisesti katsoen yhtä suuret.
Likimääräisiä geometrisia kaavoja[muokkaa | muokkaa wikitekstiä]

Jos havaitsija on lähellä Maan pintaa, lausekkeessa (2R + h) voidaan h pyöristää nollaksi, jolloin saadaan:
Koska Maan säde on noin 6371 kilometriä, on tässä esiintyvä vakio noin 3570 , ja lukuarvoyhtälönä kaava voidaan esittää muodossa
missä etäisyys d on kilometreinä ja havaitsijan silmän korkeus h metreinä.
Tämä kaava pätee, kun havaitsijan silmän korkeus on paljon pienempi kuin Maan säde, käytännössä aina silloinkin, kun havaitsija on vuoren huipulla, lentokoneessa tai kuumailmapallossa.
Täsmällinen kaava pallomaiselle Maalle[muokkaa | muokkaa wikitekstiä]
Jos havaitsija on hyvin korkealla, käytännössä Maata kiertävässä avaruusaluksessa, n silmä on hyvin korkealla, edellä olevat likimääräiskaavat eivät enää päde, vaan näköetäisyys d on
missä R on Maan säde ja h havaitsijan korkeus maan pinnasta. Molemmat on tällöin ilmoitettava samoina yksikköinä. Esimerkiksi jos avaruusalus on 2000 kilometrin korkeudella, sieltä näkee Maan päälle 5430 kilometrin päähän. Jos tässä laskussa termi h2 jätettäisiin huomiotta, tulokseksi saataisiin 5048 kilometriä, missä on 7 prosentin virhe.
Horisontin yläpuolella olevat kohteet[muokkaa | muokkaa wikitekstiä]
Edellä olevat kaavat osoittavat, kuinka kaukana oleva kohta Maan pinnasta on tietyltä korkeudelta nähtävissä. Kuinka kauas jokin Maan pinnasta kohoava kohde näkyy, voidaan laskea laskemalla toisaalta tämän kohteen huipulla mahdollisesti olevan havaitsijan horisontin etäisyys sekä sitä etäältä katsovan havaitsijan horisontin etäisyys ja laskemalla nämä etäisyydet yhteen. Esimerkiksi jos havaitsijan silmät ovat 1,7 metriä maanpinnan ympärillä, hänen horisonttinsa on 4,65 kilometrin päässä. Toisaalta sadan metrin korkuisen tornin huipulta katsottuna horisontti olisi 35,7 kilometrin päässä. Näin ollen tasaisella maalla seisova havaitsija voi nähdä tämän tornin, jos hänen etäisyytensä siitä on enintään 40,35 kilometriä. Vastaavasti veneessä oleva havaitsija, jonka silmät ovat samalla korkeudella, voi nähdä 10 metrin korkuiset puut, jos ne ovat enintään 16 kilometrin päässä.
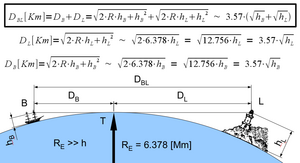
Oikealla oleva kaavio esittää laivaa ja majakkaa. Majakka näkyy laivasta käsin, jos
missä etäisyys majakkaan (DBL9 on laskettu kilometreinä, laivalla olevan havaitsijan silmien korkeus (hB) ja majakan korkeus (hL) metreinä. Jos valon taittuminen ilmakehässä otetaan huomioon, majakka näkyy, jos
Valon taittumisen vaikutus[muokkaa | muokkaa wikitekstiä]
Koska ilmakehä taittaa valoa, tasaisella maalla tai merellä voidaan usein nähdä hieman kauemmaksikin kuin edellä olevat geometriset kaavat osoittavat. Normaaleissa olosuhteissa selkeällä säällä tämä ero on noin 8 %; siihen kuitenkin vaikuttavat suuresti lämpötilan vaihtelut, varsinkin merellä, minkä vuoksi näköetäisyys voidaan laskea vain likimääräisesti.[4]
John Sweer on esittänyt horisontin etäisyydelle d lausekkeen[5]
missä RE on Maan säde, ψ horisontin kallistuma ja δ valon taittuminen horisontissa. Kallistuma voidaan määritellä lausekkeella
missä h on havaitsijan korkeus Maan pinnalta, μ ilman taitekerroin havaitsijan korkeudella ja μ0 taitekerron maan pinnalla.
Valon taittuminen voidaan laskea integraalilla
missä on valonsäteen ja Maan keskipisteen kautta kulkevan suoran välinen kulma. Kulmien ψ ja välillä on yhteys
Paljon yksinkertaisemmin voidaan likiarvoja laskea Andrew T. Youngin esittämällä tavalla käyttämällä muutoin geometrisen mallin mukaisia kaavoja mutta korvaamalla Maan säde RE vakiolla R = 7/6 RE. Tällöin horisontin etäisyys on[4]
Kun Maan säde on 6371 km, ja kun d ilmoitetaan kilometreinä ja h metreinä, saadaan
- .
mikäli d esitetään mailena ja h jalkoina on kaava muotoa,
Youngin kaavan mukaiset tulokset ovat hyvin lähellä Sweerin kaavan mukaisia ja tarpeeksi tarkkoja moniin tarkoituksiin.
Horisontin kaarevuus[muokkaa | muokkaa wikitekstiä]
Maanpinnan yläpuolelta katsottuna horisontti näyttää hieman kaarevalta, onhan se kuitenkin ympyrä. Tämän kaarevuuden , havaitsijan korkeuden h ja Maan säteen R välillä on yhteys
Kaarevuus on radiaaneina ilmoitetun kaarevuussäteen käänteisarvo. Kaarevuus 1 vastaa ympyrää, jonka kulmasäde on 45°, ja horisontin kaarevuus on näin suuri noin 2640 kilometrin korkeudelta katsottuna. Kymmenen kilometrin korkeudella lentävästä lentokoneesta katsottuna horisontin matemaattinen kaarevuus on 0,056, mikä vastaa 10 metrin säteisen ympyränkaaren näennäistä kaarevuutta 56 senttimetrin päästä katsottuna. Horisontin näennäinen kaarevuus on kuitenkin tätä pienempi, mikä johtuu valon taittumisesta ilmakehässä ja siitä, että horisontissa näkyy usein korkeita pilvikerroksia, jotka heikentävät näkyvyyttä.
Lähteet[muokkaa | muokkaa wikitekstiä]
- ↑ "ὁρίζων" A Greek-English Lexicon] perseus.tufts.edu. Viitattu 24.11.2011.
- ↑ Suomen sanojen alkuperä, Etymologinen sanakirja, 1. osa (A-K), s. 173. hakusana Horisontti. Helsinki: Suomalaisen kirjallisuuden seura, Kotimaisten kielten tutkimuskeskus, 2001. ISBN 951-717-692-9.
- ↑ Hannu Karttunen, Heikki Oja, Pekka Kröger, Markku Poutanen: Tähtitieteen perusteet, s. 28-29. Helsinki: Tähtitieteellinen yhdistys Ursa, Valtion painatuskeskus, 1984. 951-859-367-1.
- ↑ a b c Distance to the Horizon mintaka.sdsu.edu. Viitattu 23.11.2011.
- ↑ Journal of the Optical Society of America, 1938, nro 28. Artikkelin verkkoversio.
Aiheesta muualla[muokkaa | muokkaa wikitekstiä]
- Horisontin etäisyyden johto Steve Sque.
- Dip of the Horizon. Andrew T. Young.





























