Alkulukufunktio
Alkulukufunktio on matematiikan funktio, jolla lasketaan reaalilukua x pienempien tai yhtäsuurten alkulukujen lukumäärää.[1][2][3] Funktion merkintä on (Kaavassa π(x) ei viitata lukuun π.)
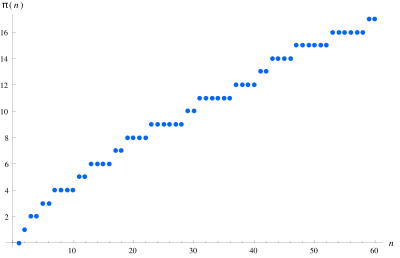
Historiaa[muokkaa | muokkaa wikitekstiä]
1700-luvulla löysivät Gauss ja Legendre että
on hyvä approksimaatio alkulukufunktiolle; tarkemmin,
Tämä lauseke tunnetaan alkulukulauseena; se todistettiin 1800-luvun lopulla oikeaksi. Väite voidaan kirjoittaa yhtäpitävästi muodossa
jossa on logaritminen integraalifunktio.
Littlewoodin lause[muokkaa | muokkaa wikitekstiä]
John Littlewood todisti 1914 että on olemassa mielivaltaisen suuria lukuja x, joille
ja mielivaltaisen suuria lukuja x, joille
Tästä seuraa että erotuksen π(x) − li(x) merkki vaihtuu äärettömän usein.
Riemannin hypoteesi[muokkaa | muokkaa wikitekstiä]
Riemannin hypoteesi on ekvivalentti seuraavaan kaavaan:
Riemannin hypoteesi siis antaisi alkulukufunktion antamalle arviolle alkulukujen määrästä huomattavasti nykyistä tiukemmat virherajat.
Lähteet[muokkaa | muokkaa wikitekstiä]
- ↑ A table of prime counts pi(x) to 1e16
- ↑ Algorithmic Number Theory, s. volume 1 page 234 section 8.8. MIT Press.
- ↑ Prime Counting Function MathWorld.








