Kultainen spiraali

Kultainen spiraali on logaritminen spiraali, jonka kasvutekijä on φ, kultainen leikkaus.[1] Siis kultainen spiraali levenee (tai etenee kauemmaksi alkupisteestään) tekijän φ verran joka neljänneskierroksella jonka se kääntyy.
Yhtälö[muokkaa | muokkaa wikitekstiä]
Kultaisen spiraalin napakoordinaattiyhtälö on sama kuin muille logaritmisille spiraaleille, mutta erikoisarvolla kasvutekijälle b:[2]
tai
jossa e on luonnollisten logaritmien kantaluku, a on mielivaltainen positiivinen reaalivakio, ja b sellainen, että θ on suora kulma (neljänneskäännös jompaankumpaan suuntaan):
Joten b on
b:n numeerinen arvo johtuu siitä onko suora kulma mitattu 90 asteena vai radiaanina; ja kun kulma voi olla kumpaan tahansa suuntaan, on helpointa kirjoittaa yhtälö b:n itseisarvolle (siis b voi olla myös tämän arvon vastaluku):
- θ:lle asteina;
- θ:lle radiaaneina.
Vaihtoehtoinen yhtälö logaritmiselle ja kultaiselle spiraalille on:[3]
jossa vakio c on:
mikä kultaiselle spiraalille antaa c:n arvot:
jos θ on mitattu asteina, ja
jos θ on mitattu radiaaneina.
Kultaisen spiraalin approksimaatioita[muokkaa | muokkaa wikitekstiä]

On useita samanlaisia spiraaleita, jotka approksimoivat, mutteivat ole täsmälleen samoja kuin kultainen spiraali.[4] Näitä usein sekoitetaan kultaiseen spiraaliin.
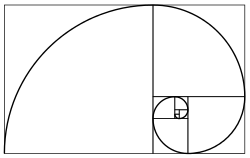
Esimerkiksi, kultaista spiraalia voidaan approksimoida "kääntyvällä suorakaide diagrammilla," jossa spiraloivien kultaisten suorakaiteiden muodostamien neliöiden vastakkaiset kulmat ovat yhdistetty neljännesympyröillä. Lopputulos on erittäin lähellä aitoa kultaista spiraalia. (Katso kuva ylimpänä oikealla).
Toinen approksimaatio on Fibonaccin spiraali, mikä ei ole aito logaritminen spiraali. Se muodostuu sarjasta neljännesympyräisiä kaaria joiden säteet ovat peräkkäin kasvavia Fibonaccin lukuja. Joka neljännes käännös Fibonaccin spiraali levenee φ:n sijasta muuttuvan tekijän, joka on yhtäsuuri kuin Fibonaccin lukujonon termin suhde edeltäjäänsä, verran. Peräkkäisten termien suhteet Fibonaccin sarjassa lähestyvät φ:tä, joten spiraalit muistuttavat toisiaan.
Spiraaleja luonnossa[muokkaa | muokkaa wikitekstiä]
Approksimaalisia logaritmisia spiraaleja voi ilmetä luonnossa (esimerkiksi spiraaligalaksien kierteissä). Helmiveneiden kuorien joskus sanotaan levenevän kultaisen spiraalin mukaisesti, ja ne liittyvät siten sekä φ:hin että Fibonaccin sarjaan. Todellisuudessa, helmiveneiden kuorissa (ja monissa nilviäisten kuorissa) esiintyy logaritmisen spiraalin mukaista kasvua, mutta eri kulmassa kuin kultaisessa spiraalissa.[5] Tämä sallii organismin kasvun muotoa muuttamatta. Spiraalit ovat yleisiä luonnossa ja kultaiset spiraalit ovat yksi erikoistapaus niistä.
Lähteet[muokkaa | muokkaa wikitekstiä]
- ↑ Chang, Yu-sung, "Golden Spiral", The Wolfram Demonstrations Project.
- ↑ Hemenway, Priya (2005). Divine Proportion: φ Phi in Art, Nature, and Science. Sterling Publishing Co, 127–129. ISBN 1402735227.
- ↑ Mainzer, Klaus (1996). Symmetries of Nature: A Handbook for Philosophy of Nature and Science. Walter de Gruyter, 45, 199–200. ISBN 3110129906.
- ↑ Madden, Charles B. (1999). Fractals in Music: introductory mathematics for musical analysis. High Art Press, 14–16. ISBN 0967172764.
- ↑ Sea Shell Spirals Science News. 1.4.2005. Society for Science & the Public. Arkistoitu 3.10.2012. Viitattu 17.10.2011.










