Yksikköjuuri

Viidennet yksikköjuuret kompleksitasossa

Kolmannet yksikköjuuret kompleksitasossa.

Yksikköjuuri tai ykkösenjuuri on kompleksiluku, joka korotettuna annetun positiivisen kokonaisluvun n osoittamaan potenssiin on 1. Toisin sanoen n:nnet yksikköjuuret ovat yhtälön

$z^{n}=1$

ratkaisuja kompleksilukujen joukossa.

Moivren ja Eulerin kaavat

Kutakin positiivista kokonaislukua n kohti on olemassa n kpl n:siä yksikkö­juuria. Ne sijaitsevat kaikki kompleksitasoon piirretyn yksikköympyrän kehällä ja muodostavat tämän ympyrän sisään piirretyn säännöllisen n-kulmion kärki­pisteet, kun yksi kärki­pisteistä on pisteessä 1. Yksikkö­juurten arvot voidaan esittää muodossa

$\cos {\frac {2\pi }{k}}+i\sin {\frac {2\pi }{k}}$

missä luku k saa kaikki kokonais­luku­arvot 0:sta n-1:een. Tämä seuraa Moivren kaavasta, jonka mukaan

$(\cos \phi +i\sin \phi )^{n}=\cos(n\phi )+i\sin(n\phi )$.

Eulerin kaavan mukaisesti nämä luvut voidaan esittää myös muodossa

$e^{\frac {2\pi ik}{n}}$ (k=0, 1, …, n-1).

Tavallisesti n:nnellä yksikköjuurella tarkoitetaan näistä luvuista nimenomaan sitä, jossa k = 1, siis lukua

$e^{\frac {2\pi i}{n}}$

Sille käytetään myös merkintää $\epsilon _{n}$.

Yksikköjuurten avulla voidaan muun muassa ratkaista yleinen binomiyhtälö

$z^{n}=q$,

missä q on mielivaltainen kompleksiluku (≠ 0). Kun q voidaan aina esittää muodossa

$q=re^{i\phi }$,

ovat yhtälön ratkaisut

$x={\sqrt[{n}]{z}}e^{\frac {i\phi }{n}}\epsilon _{n}^{k}$.

Esimerkkejä

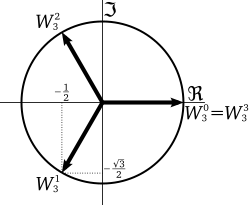
Esimerkiksi toisen yksikköjuuren arvot ovat 1 ja -1, neljännen 1, i, -1 ja -i, jotka sijaitsevat kompleksi­tasoon piirretyn neliön kärki­pisteissä. Kolmannen yksikkö­juuren (ε₃^k) arvot ovat
1 sekä $\cos {\frac {2\pi }{3}}\pm i\sin {\frac {2\pi }{3}}=-{\frac {1}{2}}\pm {\frac {\sqrt {3}}{2}}$,
jotka muodostavat tasa­sivuisen kolmion. Kuudennen yksikkö­juuren (ε₆^k) vastaavasti
1 ja -1 sekä $\pm \cos {\frac {2\pi }{3}}\pm i\sin {\frac {2\pi }{3}}=\pm {\frac {1}{2}}\pm {\frac {\sqrt {3}}{2}}$
, ja kahdeksannen (ε₈^k)
1, i, -1 ja -i sekä $\pm \cos {\frac {\pi }{4}}\pm i\sin {\frac {\pi }{4}}=\pm {\frac {1}{2}}\pm {\frac {\sqrt {2}}{2}}$.

Lähteet

• Lauri Myrberg: Differentiaali- ja integraalilaskenta osa 2 korkeakouluja varten, s. 181–182. Kirjayhtymä, 1975. ISBN 951-26-0994-0.
• Olli Lehto: Funktioteoria I–II, s. 8–10. Limes ry, 1975. ISBN 951-745-077-X.

Kirjallisuutta

• Spiegel, Murray R.; Lipschutz, Seymour; Schiller, John J.; Spellman, Dennis: Complex Variables. Shaum's Outline Series. McGraw-Hill Book Company, 2009 (1964). ISBN 978-0-07-161569-9, ISBN 978-0-07-161570-9 (eBook).
• Väisälä, Kalle: Matematiikka IV. 141, 10. painos. Espoo: Otakustantamo, 1986 (1965). ISBN 951-671-087-5.