Kiderakenne

Kiderakenne on atomien järjestys kiteisessä aineessa. Kiderakenne koostuu alkeiskopeista, jotka toistuvat tasavälisessä avaruushilassa. Alkeiskopin särmien pituuksia kutsutaan kideakseleiksi ja niiden muodostamia kulmia hilakulmiksi.
Alkeiskoppi[muokkaa | muokkaa wikitekstiä]
Alkeiskoppi on kiderakenteen perusosa. Se on pienin rakenne, jota toistamalla koko kiderakenne saadaan rakennettua. Alkeiskoppi rakentuu molekyyleistä, atomeista tai ioneista, joita voidaan kuvata kovina, pyöreinä palloina.
Kidejärjestelmä[muokkaa | muokkaa wikitekstiä]
Kidejärjestelmä on hilan pisteryhmä, joka ei sisällä atomien paikkoja alkeiskopissa. Kidejärjestelmiä on seitsemän (laskevassa symmetriajärjestyksessä), kuutiollinen, tetragoninen, heksagoninen, trigoninen, ortorombinen, monokliininen ja trikliininen.[1] Erilaisten avaruushilojen luokittelun esitti ensimmäisenä saksalainen fyysikko, professori Mauritius Ludovicus (Moritz Ludvig) Frankenheim 1835 julkaisussaan Die Lehre von der Cohäsion, umfassened die Elasticität der Gase, die Elasticität und Coharenz der flüssigen und festen Körper und die Krystallkunde, Breslau, 1835. Hän teki kuitenkin virheen (15 hilaa), jonka ranskalainen fyysikko Auguste Bravais korjasi 1848. Hän todisti olemassa olevan 14 Bravais'n hilaa.
Bravais'n hilat[muokkaa | muokkaa wikitekstiä]
Bravais'n hilat määritellään kolmella hilavektorilla (hilavakio) a, b ja c ja niiden välisillä kulmilla α, β ja γ. Koordinaatistona on yleensä oikeakätinen koordinaatisto. Bravais'n hiloja on edellä mainitut seitsemän, joiden sisällä esiintyy 1–4 variaatiota.
- kuutiollisen rakenteen alkeiskopeille pätee a=b=c ja α=β=γ=90°
- yksinkertainen kuutiollinen (engl. simple cubic, SC), atomit kuution kärkipisteissä
- tilakeskinen kuutiollinen (TKK, body-centered cubic, BCC), atomit kuution kärkipisteissä ja sen keskipisteessä
- pintakeskinen kuutiollinen (PKK, face-centered cubic, FCC), atomit kuution kärkipisteissä sekä sivutahkojen keskipisteissä
- tetragoninen a=b≠c ja α=β=γ=90° (tetragonal)
- yksinkertainen
- tilakeskinen
- ortorombinen a≠b≠c ja α=β=γ=90° (orthorhombic)
- yksinkertainen
- tilakeskinen
- päätepintakeskinen
- pintakeskinen
- trigoninen eli romboedrinen a=b=c ja α=β=γ≠90° (rhombohedral)
- heksagoninen a=b≠c ja α=β=90° ja γ=120° (hexagonal close-packing, HCP)
- monokliininen a≠b≠c ja α=β=90° ja γ≠90° (monoclinic)
- yksinkertainen
- päätepintakeskinen
- trikliininen a≠b≠c ja α≠β≠γ≠90° (triclinic)[2]
Kiderakenteen ominaisuuksia[muokkaa | muokkaa wikitekstiä]
Kiderakenteen tärkeä tekijä sen ominaisuuksien kannalta on tiivispakkauksellisuus, joka kertoo hilassa olevan tyhjän tilan määrästä, jos atomit oletetaan koviksi, pyöreiksi palloiksi. Yleisesti voidaan sanoa, että aineen kiderakenne määräytyy siten, että kiteen energia tulee mahdollisimman pieneksi.
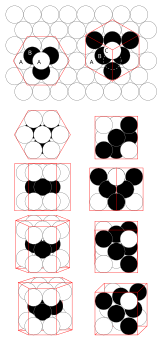
Tasossa tiivein pakkaus saadaan aikaan siten, että jokaisella atomilla on kuusi naapuriatomia, jotka muodostavat sen ympärille säännöllisen kuusikulmion. Tällaista tasoa sanotaan tiivispakkaustasoksi, ja tiivispakkaussuunta on suunta, jossa tällaisen rakenteen atomit sijaitsevat peräkkäin jonossa toisiaan koskettaen. Kolmiulotteisessa avaruudessa tiivein pakkaus saadaan Keplerin konjektuurin mukaan siten, että tällaisia tasoja pinotaan päällekkäin. Tämä voidaan tehdä kahdella tavalla. Jos ne pinotaan toisensa päälle siten, että joka toisessa atomikerroksessa atomit tulevat vastaaviin kohtiin, muodostuu heksagonaalinen tiivispakkausrakenne (ns. ABABAB-pinous). Ne voidaan kuitenkin pinota myös siten, että vain joka kolmannessa tasossa atomit sattuvat samoihin kohtiin (ns. ABCABC-pinous), jolloin syntyy pintakeskeinen kuutiollinen rakenne (PKK). Nimensä mukaisesti tämä voidaan käsittää muodostuvaksi myös kuution muotoisista yksikkökopeista, joiden halki tiivispakkaustasot kulkevat niiden avaruuslävistäjien suuntaisesti. Kiteissä voi kuitenkin esiintyä myös pinousvirheitä, jotka ovat tyypillisiä kidevirheitä.
Kolmas yleinen kiderakenne on tilakeskeinen kuutiollinen (TKK). Sitä ei voida muodostaa edellä kuvatun kaltaisista tiivispakkaustasoista, ja se onkin hieman vähemmän tiivis kuin edellä mainitut.
Tilakeskeisiä ja pintakeskeisiä kuutiollisia sekä heksagonaalisia tiivispakkausrakenteita esiintyy varsinkin metalleilla, mutta alhaisissa lämpötiloissa myös jalokaasuilla niiden esiintyessä kiinteässä olomuodossa. Sitä vastoin yksinkertainen kuutiollinen kiderakenne on harvinainen ja esiintyy alkuaineista ainoastaan poloniumilla.[3]
Timanttimainen kiderakenne on eräänlainen pintakeskisen rakenteen muunnos. Siinä on atomi kaikilla pintakeskeisen kuutiollisen kiderakenteen mukaisilla paikoilla, mutta lisäksi kuutiomaisen kopin sisällä on neljä atomia sijoittuneina kuution avaruuslävistäjille siten, että niiden etäisyys kuution kärjistä on neljäsosa avaruuslävistäjän pituudesta. Paitsi timantilla, tämä kiderakenne esiintyy myös piillä ja germaniumilla.
Koordinaatioluku ilmaisee, montako välitöntä naapuria kullakin atomilla on. Sekä pintakeskisessä kuutiollisessa(fcc) että heksagonisessa tiivispakkauksessa(hcp) koordinaatioluku on 12. Heksagonisessa tiivispakkauksessa (hcp) jokaisella atomilla on kuusi naapuria samassa tasossa sekä lisäksi kolme lähinnä ylemmässä ja kolme lähinnä alemmassa tasossa. Pintakeskisessä kuutiollisessa (fcc) tasossa jokaisen atomin lähimmät naapuriatomit ovat niiden kahdentoista neliön keskipisteessä, jotka rajoittavat kyseiseen atomiin liittyviä kuutiomaisia yksikkökoppeja. Tilakeskisessä kuutiollisessa rakenteessa koordinaatioluku on 8, yksinkertaisessa kuutiollisessa 6.
Kiderakenteella on pakkaustiheys, joka on PKK- ja heksagonisella rakenteella 74 % ja TKK-rakenteella 68 %. PKK- ja heksagonisessa rakenteessa on tiivispakkaustasoja, TKK-rakenteessa niitä ei ole. Tiivispakkaustasot toimivat usein liukutasoina plastisen muodonmuutoksen siirrosliukumisessa.
Ioniyhdisteiden kiderakenteet eroavat alkuaineiden kiderakenteista siinä, että niissä esiintyy eri alkuaineiden ioneja. Esimerkiksi ruokasuolan eli natriumkloridin kiderakenne muistuttaa yksinkertaista kuutiollista, mutta kidehilan joka toisen atomin paikalla on natrium- (Na+ ja joka toisen paikalla kloridi-ioni (Cl-) siten, että jokaisella ionilla on välittöminä naapureina kuusi vastakkaismerkkistä ionia.
Atomien väliin jäävään tyhjään tilaan voi sijoittua pienempiä välisija-atomeja. Tyhjä tila muodostaa erilaisia säännöllisiä monitahokkaita.
Katso myös[muokkaa | muokkaa wikitekstiä]
Lähteet[muokkaa | muokkaa wikitekstiä]
- Kidejärjestelmät (Arkistoitu – Internet Archive)
- Rosenberg, H. M.: The Solid State. 3rd edition. Oxford University Press, 1988. ISBN 0-19-851870-6.
Viitteet[muokkaa | muokkaa wikitekstiä]
- ↑ Geologian museo/Kivimuseo/Lehtinenlähde tarkemmin?
- ↑ ”Kidejärjestelmä”, Jalokivien maailma, s. 10–11. Tšekinkielinen alkuteos, suomennettu saksankielisestä laitoksesta. Suomentanut Kalle Taipale. WSOY, 1998. ISBN 951-0-22706-4.
- ↑ Polonium Is The Only Element With Simple Cubic Crystal Structure American Institute of Physics. Arkistoitu 17.12.2013. Viitattu 19.12.2012.
Kirjallisuutta[muokkaa | muokkaa wikitekstiä]
- Powell, Richard C.: Symmetry, Group Theory, and the Physical Properties of Crystals. Springer, 2010. ISBN 978-1-4419-7597-3. doi:10.1007/978-1-4419-7598-0. (englanniksi)
Aiheesta muualla[muokkaa | muokkaa wikitekstiä]
 Kuvia tai muita tiedostoja aiheesta Kiderakenne Wikimedia Commonsissa
Kuvia tai muita tiedostoja aiheesta Kiderakenne Wikimedia Commonsissa













