Rayleigh’n–Jeansin laki
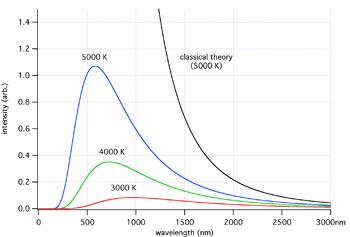
Rayleigh’n–Jeansin laki on Planckin lain approksimaatio matalilla taajuuksilla. Se kuvaa mustan kappaleen säteilytiheyden aallonpituuden funktiona:[1]
Vaihtoehtoisesti laki voidaan ilmaista taajuuden avulla muodossa
Rayleigh'n–Jeansin laki on yhteensopiva kokeellisten tulosten kanssa suurilla aallonpituuksilla (matalilla taajuuksilla). Se ei vastaa kokeita lyhyillä aallonpituuksilla (korkeilla taajuuksilla), vaan sen mukaan säteilytiheys kasvaa äärettömäksi aallonpituuden lähestyessä nollaa. Tämä ristiriita havaintojen ja klassisen fysiikan ennusteiden välillä tunnetaan yleisesti nimellä ultraviolettikatastrofi. Rayleigh'n–Jeansin laki voidaan johtaa Planckin laista taajuuksille, jotka ovat matalia verrattuna lämpötilaan ().
Historia[muokkaa | muokkaa wikitekstiä]
Gustav Kirchhoff havaitsi vuonna 1859, että hehkuvan kappaleen emissiospektrin ja sen absorptiokertoimen välinen suhde on sama kaikille samassa lämpötilassa oleville kappaleille.[2] Ideaalisen mustan kappaleen tapauksessa Kirchhoffin laki kertoo säteilyspektrin olevan ainoastaan kappaleen lämpötilasta riippuva universaali funktio.[3] Tämän universaaliuden oletettiin liittyvän perustavanlaatuisiin fysiikan lakeihin, minkä vuoksi mustan kappaleen säteilyspektrin ymmärtäminen muodostui keskeiseksi fysiikan ongelmaksi seuraavan 50 vuoden ajaksi.[4]
Brittiläinen fyysikko lordi Rayleigh johti Rayleigh'n-Jeansin lain -riippuvuuden vuonna 1900 käyttäen klassisen fysiikan energian ekvipartitioteoreemaa. Rayleigh havaitsi johtamansa yhtälön ennustavan että säteilyn intensiteetti kasvaisi korkeilla taajuuksilla rajatta, mikä ei vastannut havaintoja. Hän lisäsi sen vuoksi yhtälöönsä ylimääräisen eksponentiaalisen katkaisufunktion, joka rajoitti säteilyn intensiteettiä korkeilla taajuuksilla, mutta ei muokannut matalien taajuuksien ennustetta. Rayleigh'n esittelemänsä säteilylaki ei kuitenkaan sopinut yhteen kokeellisen datan kanssa. Täydellisemmät johdot Rayleigh'n-Jeansin laille esittivät vuonna 1905 lordi Rayleigh ja James Jeans käydessään Nature-lehden sivuilla julkista keskustelua siitä miksi laki ei vastaa kokeita. Rayleigh uskoi, että teorian ja kokeiden välinen ristiriita johtui siitä että ekvipartitioteoreema ei pätenyt korkeataajuisille värähtelyille. Jeans puolestaan uskoi ekvipartitioteoreemaan, mutta hänen mukaansa korkeataajuiset moodit eivät ehdi saavuttamaan lämpötasapainoa, minkä vuoksi tasapainotilaan perustuvat laskut ovat virheellisiä. Myös Albert Einstein johti lain itsenäisesti vuonna 1905.[5]
Rayleigh'n-Jeansin lain ei missään vaiheessa uskottu kuvaavan mustan kappaleen säteilyspektriä tarkasti, sillä sen ennusteet olivat alusta asti voimakkaasti ristiriidassa kokeellisten tulosten kanssa. Lisäksi Max Planck löysi mustan kappaleen säteilyspektriä tarkasti kaikilla taajuusalueilla kuvaavan lain jo lokakuussa 1900. Planckin alkuperäinen tavoite oli ollut löytää tyydyttävä johto Wienin säteilylaille, joka vastasi tarkasti siihenastista kokeellista dataa korkeilla taajuuksilla. Saatuaan kuitenkin tietää, että uusimmat kokeelliset tulokset eivät vastanneet Wienin säteilylain ennusteita matalilla taajuuksilla, Planck muutti laskunsa lähtöoletuksia ja johti nykyään Planckin säteilylakina tunnetun yhtälön. Planckin lain alkuperäinen johto oli epätyydyttävä, sillä se perustui matemaattiseen oletukseen, jonka fysikaalista taustaa ei ymmärretty. Vielä myöhemmin samana vuonna vuonna Max Planck johti lakinsa esittämällä uuden oletuksen, jonka mukaan värähtelymoodien energia on kvantittunut ja että ne voivat virittyä vain energiatiloille, jotka ovat tietyn minimienergian monikertoja. Oletus energian kvantittumisesta ei ollut yhteensopiva klassisen fysiikan ekvipartitioteoreeman kanssa, ja se johti myöhemmin kvanttimekaniikan kehittämiseen.[6]
Matemaattinen käsittely[muokkaa | muokkaa wikitekstiä]
Laki voidaan johtaa tarkastelemalla sähkömagneettisen kentän ominaismoodeja laatikossa, jonka sivun pituus on ja seinät ovat täydellisiä johteita.[7] Laatikon sisällä ei ole varauksenkuljettajia, jolloin sähkökentän dynamiikka noudattaa aaltoyhtälöä
Ottamalla laatikon seinien antamat reunaehdot huomioon, voidaan osoittaa että sähkökentän ominaismoodit ovat seisovia aaltoja, joiden sähkökentän komponentit ovat
missä , ja ovat sähkökentän komponenttien amplitudit, on moodin ominaistaajuus ja , ja ovat eri moodeja numeroivia kokonaislukuja. Aaltoyhtälön perusteella säteilymoodin kulmataajuus on missä on aaltovektorin itseisarvo. Säteilymoodin aallonpituus on .
Komponentit eivät ole täysin itsenäisiä, sillä sähkökenttä on lähteetön. Lähteettömyyden perusteella aaltovektori on kohtisuorassa sähkökenttää vastaan, ja jokaista aaltovektoria kohti voidaan valita vain kaksi toisiaan vastaan kohtisuoraa polarisaatiosuuntaa. Negatiiviset kokonaisluvut , ja eivät myöskään tuota lineaarisesti riippumattomia ratkaisuita. Kentän kaikki ominaismoodit luetella valitsemalla positiivisten kokonaislukujen muodostama vektori sekä yksi kahdesta polarisaatiosuunnasta.
Kentän ominaismoodien lukumäärä aallonpituusintervallia kohti saadaan muuntamalla summa ensin integraaliksi aaltovektorien yli, ja sitten vaihtamalla integroimismuuttujaa:
Etutekijä 1/8 tulee siitä, että kokonaisluvut summataan vain positiivisten lukujen yli, jolloin vastaavasti myös integraali rajoitetaan vain yhteen avaruuden oktanttiin. Tästä saadaan säteilymoodien tilatiheydeksi yksikkötilavuudessa ja aallonpituutta kohti ,
Klassisen fysiikan mukaan termodynaamisessa tasapainotilassa energia jakautuu säteilymoodien kesken siten että kullakin moodilla verran energiaa. Tämä periaate tunnetaan nimellä ekvipartitioteoreema tai energian tasajakautumisperiaate. Tasajakautumisperiaatteen perusteella sähkömagneettisen kentän energiatiheys on verrannollinen moodien lukumäärään. Näin löydetään Rayleigh'n-Jeansin lain mukainen säteilyn energiatiheys aallonpituusintervallia kohti:
Energiatiheys kasvaa voimakkaasti lyhyillä aallonpituuksilla. Kokonaisenergiatiheydeksi voidaan muodollisesti kirjoittaa
Integraali kasvaa rajatta, eli klassisen fysiikan mukaan sähkömagneettisen kentän energia ei ole äärellinen.
Kvanttimekaaninen Planckin säteilylaki voidaan johtaa pitkälti ylläolevan johdon mukaisesti. Tasajakaumaperiaatteen sijaan moodien energia lasketaan kuitenkin painottamalla ominaismoodia vastaavan säteilykvantin energiaa Bosen-Einsteinin jakaumalla.[7] Bosen-Einsteinin jakauma painottaa matalia taajuuksia ja häviää korkeilla taajuuksilla , minkä vuoksi sen tuottama energiatiheys on äärellinen.
Lain vaihtoehtoisia muotoja[muokkaa | muokkaa wikitekstiä]
Sovelluksesta riippuen voi olla luonnollisempaa tarkastella joko mustan kappaleen säteilemää tehoa tai sähkömagneettisen kentän energiatiheyttä . Molemmat näistä voidaan parametrisoida joko aallonpituuden tai taajuuden mukaan. Planckin laki ja siitä saatava Rayleigh'n-Jeansin approksimaatio voidaan siten kirjoittaa muodoissa [8][9][10][11]
Säteilytehon ja energiatiheyden välillä on relaatio . Aallonpituuden ja taajuuden funktiona parametrisoitujen funktioiden välillä on yhteys missä tekijä tulee integraalimerkin alla tehtävästä muuttujanvaihdosta.
Lähteet[muokkaa | muokkaa wikitekstiä]
- Claude Cohen-Tannoudji, Bernard Diu ja Franck Laloë: Quantum Mechanics: Volume One, s. 624–626. Paris: Hermann, 1977. (englanniksi)
Viitteet[muokkaa | muokkaa wikitekstiä]
- ↑ Kuhn, Thomas S.: Black-body theory and the quantum discontinuity, 1894-1912. Oxford : Clarendon Press ; New York : Oxford University Press, 1978. ISBN 978-0-19-502383-1. archive.org.
- ↑ Gustav Robert Kirchhoff, Über den Zusammenhang zwischen Emission und Absorption von Licht und Wärme, Monatsberichte der Akademie der Wissenschaften zu Berlin 1859 Dezember
- ↑ Gustav Kirchhoff (1860) Über das Verhältnis zwischen dem Emissionsvermögen und dem Absorptionsvermögen der Körper für Wärme und Licht. Poggendorffs Annalen der Physik 109 275-301
- ↑ Max Jammer: The conceptual development of quantum mechanics, s. 9. New York, McGraw-Hill, 1966. Teoksen verkkoversio.
- ↑ A. Pais: Einstein and the quantum theory. Reviews of Modern Physics, 1.10.1979, 51. vsk, nro 4, s. 863–914. doi:10.1103/RevModPhys.51.863. ISSN 0034-6861. Artikkelin verkkoversio. en
- ↑ Max Jammer: The conceptual development of quantum mechanics, s. 17-22. New York, McGraw-Hill, 1966. Teoksen verkkoversio.
- ↑ a b Charles Kittel and Herbert Kroemer: Thermal Physics, s. 80. W.H. Freeman and Company, 1980. Teoksen verkkoversio.
- ↑ Joseph Caniou, C. Sidery: Passive infrared detection: theory and applications, s. 117. Boston: Kluwer Acad. Publ, 1999. ISBN 978-0-7923-8532-5. Teoksen verkkoversio.
- ↑ Gerhard Kramm, Nicole Mölders: Planck's blackbody radiation law: Presentation in different domains and determination of the related dimensional constants. Journal of the Calcutta Mathematical Society, 1.1.2009. Artikkelin verkkoversio.
- ↑ Evgenij A. Šarkov: Passive microwave remote sensing of the earth: physical foundations. Berlin, Heidelberg: Springer, 2003. ISBN 978-3-540-43946-2. Teoksen verkkoversio.
- ↑ Jonathan M. Marr, Francis P. Wilkin: A better presentation of Planck’s radiation law. American Journal of Physics, 2012-05, 80. vsk, nro 5, s. 399–405. doi:10.1119/1.3696974. ISSN 0002-9505. Artikkelin verkkoversio.

























![{\displaystyle [\lambda ,\lambda +{\mathrm {d} }\lambda ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c92d12fec228c218234297d4663df533355cc5bb)











