Tetraatio

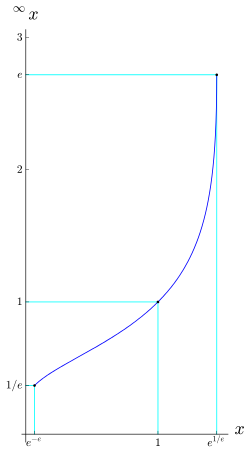
$\lim_{n\rightarrow \infty} x^{\frac{n}{}}$ Tetraatio raja-arvoilla $(e^{-1})^e \le x \le e^{e^{-1}})$

Tetraatio ("iteroitu potenssiinkorotus") on matemaattinen laskutoimitus, jossa lukua korotetaan itsensä suuruiseen potenssiin useita kertoja peräkkäin:

1. Yhteenlasku

   $a + n = a+\underbrace{1 + 1 + \cdots + 1}_n$

   a:han lisätään "1" n kertaa.

2. kertolasku

   $a \times n = \underbrace{a + a + \cdots + a}_n$

   a lisätään itseensä n kertaa.

3. potenssi

   $a^n = \underbrace{a \times a \times \cdots \times a}_n$

   a kerrotaan itsellään n kertaa.

4. Tetraatio

   ${^{n}a} = \underbrace{a^{a^{\cdot^{\cdot^{a}}}}}_n$

   a korotetaan potenssiin n kertaa.

Laskeminen

Tetraatiolla merkitään erittäin suuria potenssiinkorotuksia:

$\,\!\ ^{4}2 = 2^{2^{2^2}} = 2^{\left[2^{\left(2^2\right)}\right]} = 2^{\left(2^4\right)} = 2^{16} = 65,\!536$

On huomattava, ettei potenssiinkorotus ole liitännäinen:

$\,\! 2^{2^{2^2}} \ne \left[{\left(2^2\right)}^2\right]^2 = 2^{2 \cdot 2 \cdot2} = 256$

Esimerkkejä

$x$	${}^{2}x$	${}^{3}x$	${}^{4}x$
1	1	1	1
2	4	16	65,536
3	27	7,625,597,484,987	$\exp_{10}^3(1.09902)$
4	256	$\exp_{10}^2(2.18788)$	$\exp_{10}^3(2.18726)$
5	3,125	$\exp_{10}^2(3.33931)$	$\exp_{10}^3(3.33928)$
6	46,656	$\exp_{10}^2(4.55997)$	$\exp_{10}^3(4.55997)$
7	823,543	$\exp_{10}^2(5.84259)$	$\exp_{10}^3(5.84259)$
8	16,777,216	$\exp_{10}^2(7.18045)$	$\exp_{10}^3(7.18045)$
9	387,420,489	$\exp_{10}^2(8.56784)$	$\exp_{10}^3(8.56784)$
10	10,000,000,000	$\exp_{10}^3(1)$	$\exp_{10}^4(1)$