Lagrangen piste

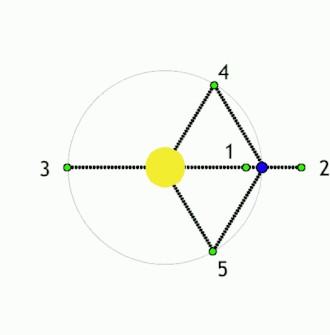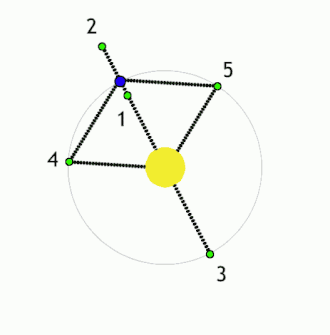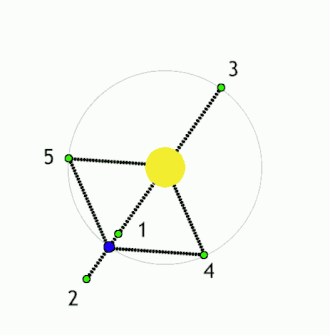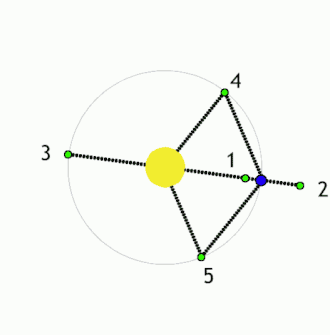
Lagrangen pisteet ovat avaruudessa olevia kohtia, joissa kahden toisiaan kiertävän massapisteen vetovoimat sekä keskipakoisvoima kumoavat toisensa niin, että kolmas, pieni massa voi pysytellä niissä paikoillaan suhteessa kahteen muuhun kappaleeseen. Kahden kappaleen muodostamaan systeemiin liittyy viisi Lagrangen pistettä[1], joista käytetään merkintöjä L1, L2, L3, L4 ja L5.[2][3][4]. Näistä L1 on kappaleiden välissä, L2 ja L3 niitä yhdistävän janan jatkeella molemmin puolin (L2 pienemmän ja L3 suuremman kappaleen takana), ja L4 ja L5 tämän suoran ulkopuolella siten, että kumpikin niistä muodostaa kappaleiden kanssa tasasivuisen kolmion.[4]
Lagrangen pisteet voidaan määrittää esimerkiksi Auringon ja jonkin planeetan tai myös planeetan ja sen kuun muodostamalle systeemille. Esimerkiksi Maan ja Kuun välissä on ns. libraatiopiste L1 ja Kuun takana L2. [5] Tunnettuja ovat myös Auringon ja Jupiterin muodostaman systeemin Lagrangen pisteet L4 ja L5, joissa sijaitsevat troijalaiset asteroidit. Jos kappale sijaitsee lähellä Lagrangen pistettä, sen rata on niin sanottu hevosenkenkärata eli se huojuu Lagrangen pisteen yli.
Lagrangen pisteet on nimetty ranskalaisen matemaatikon Joseph-Louis Lagrangen mukaan, joka keksi ne vuonna 1772 tutkiessaan kolmen kappaleen ongelmaa.[5]
Maan ja Auringon Lagrangen pisteet[muokkaa | muokkaa wikitekstiä]
Maalla ja Auringolla Lagrangen pisteitä on yhteensä viisi kappaletta: Maan ja Auringon muodostamalla suoralla kolme kappaletta (L1 Maan ja Auringon välissä ja L2 Maan takana, L3 Auringon takana lähellä Maan kiertorataa). Pistettä L1 on käytetty vuodesta 1995 Aurinkoa tarkkailevan SOHO-satelliitin kiertoradan keskipisteenä, ja se sijaitsee puolentoista miljoonan kilometrin päässä Maasta. Piste L2 sijaitsee siis Auringosta katsoen Maan takana ja on siten oivallinen paikka avaruusteleskoopille, koska kirkkaat valonlähteet Maa ja Aurinko ovat helposti peitettävissä. Lukuisten viivästysten jälkeen NASAn James Webb Space Telescopen (JWST) laukaistiin kohti L2-pistettä joulukuussa 2021. L3-piste sijaitsee hieman Maapallon radan ulkopuolella, Maasta katsottuna Auringon takana. L4 ja L5 -pisteet sijaitsevat hieman Maapallon radan ulkopuolella, mutta 150 miljoonan kilometrin etäisyydellä. Maan, Auringon ja pisteen L4 tai L5 välinen kulma on aina 60 astetta. Toisin sanoen Maa, Aurinko ja L4 tai L5 muodostavat tasasivuisen kolmion. L4:n ja L5:n keskietäisyys Maasta siis vastaa Maan keskietäisyyttä Auringosta
Näitä pisteitä käytetään satelliittien sijoituspaikkoina, sillä radankorjauksia ei juurikaan tarvitse tehdä, säästäen näin polttoainetta ja jättäen tilaa arvokkaammalle lastille, kuten tieteellisille instrumenteille.
Lagrangen pisteiden L1 ja L2 etäisyyden likimääräinen laskukaava[muokkaa | muokkaa wikitekstiä]
Jos pienemmän kappaleen massa (M2) on huomattavasti pienempi kuin suuremman kappaleen massa (M1), ovat Lagrangen pisteet L1 ja L2 suunnilleen yhtä kaukana pienemmästä kappaleesta sen molemmin puolin, kumpikin etäisyydellä
- ,
missä R on massojen M1 ja M2 välinen etäisyys.
Esimerkiksi:
- Aurinko ja Maa: Lagrangen piste L1 1 500 000 km Maasta Aurinkoon ja L2 1 500 000 km Maasta Auringosta poispäin.
- Maa ja Kuu: L1 61 500 km kuun edessä ja L2 61 500 km Kuun keskipisteen takana
Lagrangen pisteiden laskennasta ja vakaudesta[muokkaa | muokkaa wikitekstiä]
Lagrangen pisteiden laskenta perustuu Hamiltonin mekaniikkaan. Laskennassa käytetään Jacobin integraalia. Pisteet L1, L2 ja L3 ovat epävakaita, niin sanotut troijalaiset pisteet L4 ja L5 melko vakaita.[4] Näiden ympärillä on melko kaukana vakaita ratoja. Jos satelliitti, luotain tai avaruusalus viedään pisteisin L1–L3, vaaditaan jatkuvia radankorjauksia, jotta pystytään pysymään näissä pisteissä.
Lähteet[muokkaa | muokkaa wikitekstiä]
- ↑ Lagrangian point. The American Heritage® Dictionary of the English Language, Fourth Edition. Houghton Mifflin Company, 2004. Answers.com. Arkistoitu 15.4.2011. Viitattu 15.6.2010. (englanniksi)
- ↑ Stockton, J. R.: Gravity 4. Merlyn.demon.co.uk. 8.3.2010. Arkistoitu 24.3.2010. Viitattu 15.6.2010. (englanniksi)
- ↑ Spergel, David N. & Hinshaw, Gary & Bennett, Charles L.: The Lagrange Points. Microwave Anisotropy Probe (MAP). 21.5.1999. Arkistoitu 24.7.2010. Viitattu 15.6.2010. (englanniksi)
- ↑ a b c WMAP Observatory: Lagrange Points Wilkinson Microwave Anisotropy Probe – Nasa. heinäkuu 2012. Viitattu 15.6.2010. (englanniksi)
- ↑ a b What are Lagrange points? 12.2.2009. European Space Agency – ESA. Viitattu 15.6. 2010. (englanniksi)
![{\displaystyle r\approx R{\sqrt[{3}]{\frac {M_{2}}{3M_{1}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1175643479ba922598c78a6d4dfcf7fff160bfe7)
