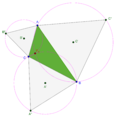
Fermat’n pisteet

Fermat’n pisteet liittyvät geometriassa kolmioihin ja sen vanhin esitys liittyy Pierre de Fermat’n kirjeeseen ystävälleen Evangelista Torricellille. Siinä esitetty probleema, jota voidaan kutsua Fermat-Steiner-probleemaksi [1], kertoi kolmesta kylästä, joista tuli suunnitella suorat tiet niiden keskellä olevaan risteykseen siten, että maanteiden yhteispituus olisi mahdollisimman lyhyt. Kun kylät sijoitetaan kolmion kärkiin, sijaitsee janojen risteys pisteessä, jota kutsutaan Fermat’n pisteeksi (tarkemmin: ensimmäinen Fermat’n piste). Koska Torricelli ratkaisi probleeman, kutsutaan pistettä myös Torricellin pisteeksi, mutta toisinaan myös ensimmäiseksi isogooniseksi pisteeksi tai Steinerin pisteeksi.[2] Piirroksissa pistettä merkitään usein X tai F1, ja se on luetteloitu Kimberlingin merkillisten pisteiden luettelossa tunnuksella .[3][4][5][6]
Fermat’n piste löytyy muillakin tavoilla. Kun kolmion sivuille piirretään tasasivuiset kolmiot siten, että niiden sivut yhtyvät alkuperäisen kolmion kanssa. Tilanne on rakenteeltaan samanlainen konstruktio, jota Napoleonin lause käsittelee. Kun kolmion kärjet yhdistetään janoilla vastaisen sivun tasasivuisen kolmion vapaaseen kärkeen, leikkaavat janat Fermat’n pisteessä. Fermat’n piste syntyy myös tasasivuisia kolmioita ympäröivien ympyröiden leikatessa toisensa.[5][6]
Ensimmäinen Fermat’n piste[muokkaa | muokkaa wikitekstiä]
Fermat’n piste sijaitsee kohdassa, missä tieverkon etäisyyksien summa saa pienimmän arvonsa: . Tarkasteltaessa tilannetta Napoleonin lauseen konstruktiossa, on tieverkon pituus sama kuin janat , jotka siis ovat yhtä pitkät. Jos kolmion kaikki kulmat ovat alle 120° niin janat, jotka yhdistävät kolmion kärjet Fermat’n pisteeseen F1, muodostavat keskenään 120° kulmat. Tällaista ominaisuutta kutsutaan isogoniseksi.[3][7]
Fermat’n piste voidaan löytää fysikaalisesti kokeilemalla. Tällöin porataan kolmion kärkiin pienet reiät, johon pujotetaan punnuksiin sidotut langat. Lankojen päät yhdistetään solmulla ja punnusten annetaan riippua samalla, kun kolmiota liikutellaan varovasti. Solmu hakeutuu asemaan, jossa lankojen suuntaiset vinot voimat lopulta kumoavat toisensa, mikä sijaitsee Fermat’n pisteessä.[3]
Jos kolmion sivun pituudet ovat a, b ja c, ja kolmion kärkien etäisyydet Fermat’n pisteestä x, y ja z, on olemassa toinen tasasivuinen kolmio, jonka sivun pituus on x + y + z, ja sen sisällä piste P siten, että etäisyydet tasasivuisen kolmion kärkiin ovat a, b ja c.[3]
Pisteen trilineaariset koordinaatit ovat
ja sen barysentriset koordinaatit ovat (A = kolmion ala)
-
Ensimmäinen Fermat’n piste F1, kun kulma C on 120 astetta. Se yhtyy kulman C kärjen kanssa.
-
Ensimmäinen Fermat’n piste F1, kun kulma C on yli 120 astetta. Piste sijaitsee kolmion ulkopuolella, useimmiten tasasivuisten kolmioiden välissä.
-
Ensimmäinen Fermat’n piste F1 määriteltynä käyttäen tasasivuisten kolmioiden ympyröitä.
-
Janat ja ympyrät yhdessä.
Toinen Fermat’n piste[muokkaa | muokkaa wikitekstiä]
Toinen Fermat’n piste (merkitään usein X', F2 tai ) syntyy samalla tavalla kuin ensimmäinenkin piste, mutta sillä erolla, että tasasivuiset kolmiot on käännetty kolmion päälle. Nyt kolmion kärjen ja sen vastaisen sivun tasasivuisen kolmion vapaan kärjen välisen janan jatkeet leikkaavat toisensa yhteisessä pisteessä. Pistettä kutsutaan myös nimellä toinen isogoninen piste.[8]
Piste F2 löytyy myös ympyröillä. Konstruktion jokaisen tasasivuisen kolmion ympäri piirretään ympyrät, jotka sitten leikkaavat toisessa Fermat’n pisteessä.[8] Pisteellä F2 on vielä eräs erikoisominaisuus. Jos yksi kulma, esimerkiksi C, on alle 60°, ja kaksi muuta kulmaa A ja B ovat yli 60°, on lausekkeella arvo minimissään. Jos kulmaehdot eivät täyty, on minimilauseke pienin jonkin muun kulman suhteen.[3]
Pisteen trilineaariset koordinaatit ovat
ja sen barysentriset koordinaatit ovat (A = kolmion ala)
-
Toinen Fermat’n piste, kun C on suuri.
-
Toinen Fermat’n piste, kun kolmio on teräväkulmainen ja F2 yhtyy tasasivuisen kolmion kärjen B kanssa.
-
Toinen Fermat’n piste, kun kulma B on 60 astetta ja F2 siihen.
Fermat'n pisteen historia[muokkaa | muokkaa wikitekstiä]
Pierre de Fermat (1601–1665)[9] kävi kirjeenvaihtoa Evangelista Torricellin (1608–1647)[10] kanssa ja haastoi hänet keksimään ratkaisun ongelmaan, jossa kolme kylää tuli yhdistää kolmella tiellä siten, että ne yhtyvät samassa pisteessä ja että teiden yhteispituus olisi pienin mahdollinen. Koska Torricelli ratkaisi ongelman vuonna 1640[2] (Viviani julkaisi sen vuonna 1659), kutsutaan toisinaan tuota pistettä Torricellin pisteeksi. Fermat’n ongelma rajoittui kolmioon, jonka kaikki kulmat olivat alle 120°, vaikka ongelma toimii muillekin kulmille.[7] Heinen todisti lauseen täydellisesti vuonna 1834.[2][5][3][11]
Ensimmäinen Fermat’n piste on ensimmäinen merkillinen piste, joka löydettiin antiikin aikojen jälkeen. Tämä on poikkeuksellisen pitkä aika, koska nykyään niitä tiedetään olevan yli 5 000.[7][4]
Muita ominaisuuksia[muokkaa | muokkaa wikitekstiä]
- Ensimmäinen Fermat’n piste () on isogonaalinen konjugaatti ensimmäisen isodynaamisen pisteen () kanssa. Se on isotominen konjugaatti merkillisen pisteen kanssa.[4]
- Toinen Fermat’n piste () on isogonaalinen konjugaatti toisen isodynaamisen pisteen () kanssa. Se on isotominen konjugaatti merkillisen pisteen kanssa.[4]
Katso myös[muokkaa | muokkaa wikitekstiä]
- Napoleonin lauseen konstruktioon liittyvät myös Napoleonin pisteet, jotka ovat kolmion merkillisiä pisteitä.
Lähteet[muokkaa | muokkaa wikitekstiä]
- Wells, David: The Penquin Dictionary of Curious and Interesting Geometry. Englanti: Penguin Group, 1991. ISBN 0-14-011813-6. (englanniksi)
Viitteet[muokkaa | muokkaa wikitekstiä]
- ↑ Gueron, Shay & Tessler, Ran: The Fermat-Steiner-problem
- ↑ a b c Harju, Tero: Geometria: lyhyt kurssi (pdf) (luentomoniste) users.utu.fi. 2007. Turun yliopisto. Viitattu 12.5.2012. [vanhentunut linkki]
- ↑ a b c d e f Wells, David: The Penquin Dictionary of Curious and Interesting Geometry, 1991, s.75
- ↑ a b c d e f g h Kimberling, Clark: Encyclopedia (html) Tekijän kotisivut. 2013. Evansville: Evansvillen Yliopisto. Viitattu 20.4.2013. (englanniksi)
- ↑ a b c d Weisstein, Eric W.: Fermat Points (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
- ↑ a b Weisstein, Eric W.: First Fermat Point (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
- ↑ a b c Koivulahti, Perttu: Trilineaariset koordinaatit (pdf) (tutkielma) 2012. Jyväskylä: Jyväskylän Yliopisto. Viitattu 20.4.2013.
- ↑ a b c Weisstein, Eric W.: Second Fermat Point (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
- ↑ Peter John Hilton, Derek Allan Holton & Jean Pedersen: Mathematical vistas: from a room with many windows, s. 27. Springer, 2002. ISBN 9780387950648. Google Book. (englanniksi)
- ↑ O'Connor, John J.; Robertson, Edmund F.: Evangelista Torricelli (sivustosta MacTutor History of Mathematics archive) University of St Andrews. Viitattu 12.5.2013. (englanniksi)
- ↑ J Krarup and S Vajda, On Torricelli's geometrical solution to a problem of Fermat, Duality in practice, IMA J. Math. Appl. Bus. Indust. 8 (3) (1997), 215-224.
Aiheesta muualla[muokkaa | muokkaa wikitekstiä]
- PlanetMath: Fermat−Torricelli theorem
- PlanetMath: Triangle center
- Ballew, Pat: The Fermat Point (Arkistoitu – Internet Archive)
- Royster, David C.: MA 341 – Topics in Geometry Lecture 17, University of Kentucky