Pintaenergia
Pintaenergiaksi kutsutaan kiinteän aineen tai nesteen ja kaasun väliseen rajapintaan sitoutunutta energiaa. Yksi sen esiintymismuodoista on nesteen pintajännitys. Pintaenergiaa kuvaava mittayksikkö on joulea neliömetrillä eli J/m².
Pinnassa olevilla molekyyleillä on enemmän energiaa kuin materiaalin sisäosissa olevilla molekyyleillä, eli molekyylin on energeettisesti suotuisaa olla materiaalin sisällä. Jos näin ei olisi, molekyylit pyrkisivät pois bulkkimateriaalista muodostaakseen uusia pintoja. Pintaenergia voidaan siksi määritellä ylimääräiseksi energiaksi verrattuna materiaalin sisäosien energiaan.
Nesteille pintajännitys ja pintaenergian tiheys ovat identtisiä. Veden pintaenergian tiheys on 0,072 J/m² ja pintajännitys 0,072 N/m; yksiköt ovat toisiaan vastaavat, mutta vain ilmaistu toisin. Kun liuos on muodostettu kahdesta nesteestä tai kiinteän aineen liuoksesta, pintajännityksen arvo voi poiketa vastaavasta puhtaan nesteen arvosta. Tätä ilmiötä voidaan kuvata Gibbsin isotermillä.[1]
Pintaenergian määrittäminen
[muokkaa | muokkaa wikitekstiä]Kun kiinteä aine leikataan osiin, sen sidokset katkeavat, mikä kuluttaa energiaa. Jos leikkaus tehdään reversiibelisti, niin energian säilymisen lain mukaan leikkaamiseen kulutettu energia on yhtä suuri kuin kahden muodostuvan pinnan energia. Materiaalin yksikköpintaenergia olisi silloin puolet sen koheesioenergiasta. Käytännössä tämä toteutuu vain tyhjiöön muodostuneella pinnalla.[1]
Nesteiden pintaenergia voidaan mitata venyttämällä nestekalvoa, mikä lisää pinnan pinta-alaa ja siten myös pintaenergiaa. Jotta nestemassan pinta-alaa voitaisiin lisätä määrällä , tarvitsee tehdä tietty määrä työtä ( tarkoittaa nesteen pintaenergian tiheyttä). Tätä menetelmää ei kuitenkaan voida käyttää kiinteiden aineiden pintaenergian mittaamiseen, koska venytettäessä kiinteän aineen kalvoa elastinen energia indusoituu materiaalin sisäosiin samalla, kun pintaenergia kasvaa.
Yleensä kiinteiden aineiden pintaenergia mitataan korkeissa lämpötiloissa. Tällöin kiinteä aine viruu, jolloin sen pinta-ala muuttuu. Tästä huolimatta tilavuus pysyy lähes samana. Jos on pintaenergian tiheys sylinterille, jonka säde on , pituus ja yksiaksiaalinen jännitys on vakio, niin tasapainossa Gibbsin energia voidaan laskea kaavalla:
Pintaenergian tiheys voidaan laskea jännityksen, säteen ja pituuden avulla kaavasta
Tämä menetelmä on pätevä vain, jos kiinteä aine on isotrooppinen eli pintaenergia on sama kaikille kristallografisille suunnille.[1]
Välifaasien termodynamiikkaa
[muokkaa | muokkaa wikitekstiä]

Välifaasin läsnäolo vaikuttaa yleisesti kaikkiin systeemin termodynaamisiin parametreihin. Välifaaseja kuvataan yleensä kahden mallin avulla, jotka ovat Gibbsin ideaali välifaasi -malli ja Guggenheimin malli. Jotta välifaasisysteemin termodynamiikkaa voidaan kuvata Gibbsin mallin avulla, systeemi täytyy jakaa kolmeen osaan: kahteen toisiinsa sekoittumattomaan nesteeseen, joiden tilavuudet ovat ja sekä nesteet toisistaan erottavaan äärettömän ohueen rajakerrokseen, jota kutsutaan Gibbsin jakavaksi tasoksi ( ).
Systeemin kokonaistilavuus on siis:
Kaikki systeemin ekstensiivisuureet voidaan kirjoittaa kolmen komponentin, bulkkifaasin , bulkkifaasin ja välifaasin summana. Ekstensiivisuureita ovat esimerkiksi sisäenergia (), molekyylien lukumäärä aineessa () ja entropia ().
Kostuminen
[muokkaa | muokkaa wikitekstiä]Kiinteällä aineella on korkea pintaenergia, jos se on muodostunut kovalenttisin sidoksin, ionisidoksin tai se on metalli. Kiteisillä aineilla, joissa molekyylien välillä on van der Waalsin voimia tai vetysidoksia, on matala pintaenergia. Kostutus tapahtuu parhaiten silloin, kun alustan pintaenergia on suuri ja kostuttavan aineen pintaenergia pieni. Esimerkiksi maalin kostuttavuutta voidaan parantaa lisäämällä siihen erilaisia lisäaineita, jotka alentavat sen pintaenergiaa. Kostutettavan pinnan kostumista voidaan parantaa esimerkiksi puhdistamalla pintaa.[2]
Pintaenergian arvoja
[muokkaa | muokkaa wikitekstiä]| Material | Pintaenergia (mJ/m²) |
|---|---|
| Lasi | 2000-4000[3] |
| Kupari | 1650[4] |
| Magnesiumoksidi | 1200[5] |
| Kalsiumfluoridi | 450[5] |
| Litiumfluoridi | 340[5] |
| Kalsiumkarbonaatti | 230[5] |
| Natriumkloridi | 300[6] |
| Kaliumkloridi | 110[6] |
| Bariumfluoridi | 280[5] |
| Pii | 1240[5] |
Leviämisparametri:
Esimerkiksi maalin, musteen tai väriaineen leviäminen kiinteälle pinnalle riippuu nesteen kyvystä kostuttaa kiinteä alusta. Jos kiinteän alustan pintaenergia muuttuu, kun siihen tiputetaan nestepisara, sanotaan että neste kostuttaa alustan. Nestepisaran leviäminen voidaan määritellä seuraavasti:
missä on leviämisparametri, on kiinteän pinnan pintaenergia, on nesteen pintaenergia ja on kiinteän pinnan ja nesteen rajapinnan interfasiaalinen energia.
Kontaktikulma:
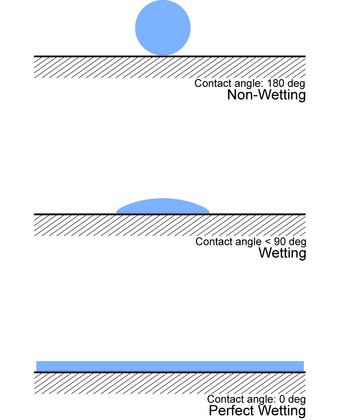
Kontaktikulman () avulla voidaan tutkia sulan kykyä kostuttaa alustansa. Kontaktikulma on kiinteän aineen ja kaasufaasin välisen rajapinnan ja nesteen ja kiinteän aineen rajapinnan välinen kulma. Kostutus on joko osittaista, jolloin neste jää pisaraksi kiinteän aineen pinnalle, tai täydellistä, jolloin neste leviää täysin kiinteän aineen pinnalle.
- Jos , neste kostuttaa alustan täysin.
- Jos , kostumista tapahtuu paljon.
- Jos , kostumista tapahtuu vähän.
- Jos , neste ei kostuta pintaa lainkaan.
Youngin yhtälö ilmaisee kontaktikulman ja interfasiaalisen energian välisen yhteyden:
missä on substraatin ja kaasufaasin välinen interfasiaalinen energia, on substraatin ja nesteen välinen interfasiaalinen energia ja on neste- ja kaasufaasin välinen interfasiaalinen energia ja on kontaktikulma.[2]
Mittausmenetelmiä
[muokkaa | muokkaa wikitekstiä]- Pääartikkeli: Kontaktikulman mittaaminen
Goniometri
[muokkaa | muokkaa wikitekstiä]
Goniometri on laite, jonka avulla voidaan analysoida pisaran geometriaa ja määrittää näin tutkittavan nesteen kontaktikulma ja pintajännitys. Pintaenergia voidaan laskea mitatun pintajännityksen ja nesteen ja pinnan välisen kontaktikulman avulla.
Pintajännityksen laskemiseksi kaasufaasin ja kiinteän pinnan välinen jännitys mitataan käyttäen referenssinesteitä (esim. vesi tai glyseroli). Analysoitava neste siirretään ruiskulla laitteessa olevalle tarkastelupinnalle ja pisarasta otetaan yksittäinen kuva tai useita kuvia, joista tehdään elokuva. Filmin data digitalisoidaan harmaaskaalakuviksi, joita analysoimalla voidaan määrittää esimerkiksi nesteen ja pinnan välinen kontaktikulma ja nesteen pintajännitys.
Pintajännitys määritetään sovittamalla Young-Laplace -yhtälö pisaran muotoon. Kontaktikulma mitataan laskemalla kulmakerroin pisaran tangentille suhteessa kiinteään tasoon. Mittauksissa oletetaan, että pisara on symmetrinen pisaran keskellä olevan pystysuoran akselin ympärillä eli oletetaan, että pisaran tarkastelusuunnalla ei ole väliä. Menetelmässä oletetaan myös, että viskositeetti tai inertia ei vaikuta pisaran muotoon vaan ainoastaan faasien välien jännitys ja painovoima muovaavat pisaraa.
Goniometri kalibroidaan tekemällä optinen suurennos. Kalibrointi voidaan tehdä korkealla tarkkuudella ja se on helppo jäljittää kansainvälisiin standardeihin. Laitteessa olevien kiinteiden pintojen ei tarvitse olla erityisen puhtaita, koska niiden kostuvuus ei sinänsä vaikuta mittaustulokseen. Tämä on merkittävä etu esimerkiksi Wihelmyn levy-menetelmään nähden, jossa pinnan täytyy olla hyvin puhdas.[7]
Wilhelmyn levy-menetelmä
[muokkaa | muokkaa wikitekstiä]Kontaktikulmaa voidaan mitata myös Wilhelmyn levy-menetelmällä. Menetelmässä tutkittavan nesteen rajapintaa kohtisuoraan suunnattu levy upotetaan nesteeseen. Tämän jälkeen nesteastiaa liikutetaan alaspäin, jolloin levy nousee nesteestä, ja nesteen levyyn kohdistama voima mitataan tensiometrillä. Mitatun voiman avulla voidaan laskea kontaktikulma seuraavalla yhtälöllä
jossa F on tensiometrillä mitattu kokonaisvoima, on nosteen aiheuttama voima, joka syntyy, kun levy upotetaan nesteeseen, on levyn pituus ja on nesteen pintajännitys.
Wilhelmyn levy-menetelmällä saadaan melko objektiivisia mittaustuloksia, joiden perusteella voidaan laskea tarkkoja keskiarvoja. Mittauksissa käytetyllä levyllä täytyy olla yhtenäinen poikkileikkaus ja levyn pituus täytyy mitata tarkasti. Menetelmä toimii vain, jos levyn molemmat puolet ovat identtiset.[8]
Kelvinin yhtälö
[muokkaa | muokkaa wikitekstiä]Nesteet pyrkivät luontaisesti tilaan, missä pintajännitys ja pintaenergia ovat mahdollisimman pieniä. Tämän vuoksi ne muodostavat kaarevia pintoja, kuplia ja pisaroita, jotta pinta-ala olisi mahdollisimman pieni. Gibbsin vapaa energia on tällöin mahdollisimman pieni. Kelvinin yhtälön avulla kuvataan höyrynpaineen muutosta
- ,
missä on kaarevan pinnan höyrynpaine, on tasaisen pinnan höyrynpaine, on pintajännitys, on nesteen moolinen tilavuus, on yleinen kaasuvakio, on lämpötila (K) ja ja ovat pinnan kaarevuus. Yhtälöä voidaan yksinkertaistaa, kun tarkastellaan nestepisaraa tai kuplaa. Voidaan olettaa, että kuplan ulkopuolinen rajapinta on samanmuotoinen sekä ulkoa että sisältä tarkasteltuna eli = , jolloin yhtälö voidaan kirjoittaa muotoon
Lähteet
[muokkaa | muokkaa wikitekstiä]- ↑ a b c D.P. Woodruff, ed. "The Chemical Physics of Solid Surfaces", Vol. 10, Elsevier, 2002.
- ↑ a b de Gennes, P G (1985). “Wetting: statics and dynamics”. Reviews of Modern Physics 57: 827-863.
- ↑ Roesler, F. C. (1956) Proc. Phys. Soc., B69, 981.
- ↑ Udin, H. (1951) J. Metals, 3, 63
- ↑ a b c d e f Gilman, J. J. (1960) J. Appl. Phys., 36, 1374.
- ↑ a b Butt, Hans-Jürgen, Kh Graf, and Michael Kappl. Physics and Chemistry of Interfaces. Weinheim: Wiley-VCH, 2006. Print.
- ↑ Polymer Engineering & Colloid Sciences, IIT Madras, Goniometer. http://www.che.iitm.ac.in/pecs/content/goniometer (Arkistoitu – Internet Archive)
- ↑ Christopher Rullison, "So You Want to Measure Surface Energy?". Kruss Laboratories technical memo.
- ↑ Jane A.W Elliot, on the complete Kelvin equation, University of Alberta, Edmonton, AB, Canada, ChE Division of ASEE 2001 http://ufdcimages.uflib.ufl.edu/AA/00/00/03/83/00152/AA00000383_00152_00274.pdf (Arkistoitu – Internet Archive)












































