Karvapallolause

Wikipediasta
Siirry navigaatioon Siirry hakuun
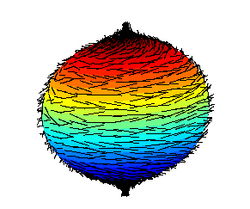
Epäonnistunut yritys kammata karvainen pallo sileäksi, tuloksena molemmille navoille jääneet tupsut.

Algebrallisen topologian karvapallolause sanoo, että jokainen pallopinnan jatkuva tangenttivektorikenttä katoaa ainakin yhdessä pisteessä. Siis jos f on jatkuva kuvaus 2-pallolta S2 avaruuteen R3, niin jossakin pallon pisteessä p kuvaus f(p)=0. Lauseen esitti Henri Poincaré 1800-luvun lopulla ja todisti ensimmäisenä Brouwer vuonna 1912. [1]

Tangenttivektorikentän nollapiste esitettynä lapsen hiuksissa.
Karvainen torus on helppo saada sileäksi.

Käytännön johtopäätöksiä[muokkaa | muokkaa wikitekstiä]

Lauseelle saadaan säätieteellinen tulkinta ajattelemalla tuulta maanpinnan tangenttivektorikenttänä. Lauseen mukaan aina jossakin maan pinnalla on täysin tyyntä.[2]

Lauseen nimi viittaa siihen johtopäätökseen, ettei karvaisen pallon tukkaa voi kammata täysin sileäksi, koska loppujen lopuksi aina johonkin kohtaan muodostuu hiuspyörre.lähde?

Lähteet[muokkaa | muokkaa wikitekstiä]

  1. ↑ Marian Gidea, Keith Burns: Differential Geometry and Topology: With a View to Dynamical Systems 2005. CRC Press. (englanniksi)
  2. ↑ Weisstein, Eric W.: Hairy Ball Theorem MathWorld, A Wolfram Web Resource. Viitattu 14.7.2020. (englanniksi)
Noudettu kohteesta ”https://fi.wikipedia.org/w/index.php?title=Karvapallolause&oldid=20594676”