Wheatstonen silta
Wheatstonen silta on sähkötekniikassa menetelmä vastuksen resistanssin määrittämiseksi. Menetelmän keksi Samuel Hunter Christien vuonna 1833. Menetelmän parannetun version teki myöhemmin tunnetuksi Charles Wheatstone vuonna 1843.[1][2]
Rakenne[muokkaa | muokkaa wikitekstiä]
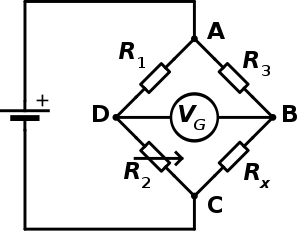
Wheatstonen siltakytkennässä on tutkittava komponentti, sekä kolme muuta vastusta joiden resistanssit tunnetaan, galvanometri ja virtalähde. Yksi tunnetuista resistansseista voidaan säätää siten, että galvanometri näyttää nollaa.[2]
Tuntemattoman vastuksen määritys[muokkaa | muokkaa wikitekstiä]
Kuvassa on tuntematon resistanssi, joka halutaan määrittää. Resistanssit , ja ovat tunnettuja sekä lisäksi resistanssia voidaan säätää. Tämän arvoa säädetään, kunnes kuvan pisteiden D ja B välillä ei ole enää jännite-eroa ja näin niiden välillä ei kulje virtaa.
Kun pisteiden B ja D välillä ei kulje virtaa, niin Kirchhoffin lain mukaisesti voidaan päätellä, että sama virta kulkee sekä vastuksen että vastuksen kautta. Samoin virta kulkee sekä vastuksen että vastuksen kautta.
Jännitelähteen positiivisen navan ja pisteen D välinen jännite-ero on sama kuin positiivisen navan ja pisteen B jännite-ero , mistä saadaan yhtälö
- .
Vastaavasti jännitelähteen negatiivisen navan ja pisteen D jännite-ero on sama kuin negatiivisen navan ja pisteen B välinen jännite-ero , joten
- .
Tuntemattoman vastuksen arvoksi saadaan[3]
- .
Piirin haarojen välinen nollavirta voidaan todeta käyttämällä herkkää galvanometriä.[2]
Lähteet[muokkaa | muokkaa wikitekstiä]
- ↑ Lindell, Ismo: Sähkön pitkä historia, s. 153–155. Helsinki: Otatieto, 2009. ISBN 978-951-672-358-0.
- ↑ a b c Inkinen, Pentti & Manninen, Reijo & Tuohi, Jukka: Momentti 2 – Insinöörifysiikka. Helsinki: Otava, 2003. ISBN 951-1-18457-1.
- ↑ Aumala, Olli: Mittaustekniikan perusteet, s. 114. Otatieto, 2001. ISBN 951-672-306-3.












