Hydrostatiikka
Hydrostatiikka on virtausmekaniikan osa-alue, joka tutkii levossa olevia nesteitä (yleisemmin fluideja eli nesteiden lisäksi myös kaasuja). Liikkuvia fluideja tutkii virtausdynamiikka, fluidien ominaisuuksia ja tehonsiirtoa hydrauliikka.
Tärkeä hydrostatiikan sovellus ovat hydrostaattiset kuormitukset eli kuormitukset, jotka hydrostaattinen paine aiheuttaa vedessä oleviin rakenteisiin. Fluidit aiheuttavat kohtisuoran paineen kaikkiin pintoihin. Jos fluidi on lisäksi levossa, paine on isotrooppinen eli suunnasta riippumaton. Kappaleen ylä- ja alapintoihin kohdistuvien painevoimien ero aiheuttaa fluidissa olevaan kappaleeseen ylöspäin suuntautuvan voiman, nosteen.
Hydrostatiikan lakeja muotoilivat ensimmäisinä muun muassa ranskalainen Blaise Pascal sekä Galileo Galilei.
Hydrostatiikan perusyhtälö[muokkaa | muokkaa wikitekstiä]
Hydrostatiikan perusyhtälö on , missä
- p on hydrostaattinen paine
- ρ on nesteen tiheys
- g on painovoimakiihtyvyys
- z on pystysuuntainen koordinaattiakseli (kuinka syvällä ollaan)
Hydrostatiikan perusyhtälön johto[muokkaa | muokkaa wikitekstiä]
Hydrostatiikan peruslähtökohta on levossa oleva tila, jolloin kappaleeseen vaikuttavien voimien summa on nolla Newtonin toisen lain mukaan. Kappaleena tarkastellaan tässä pientä nestepartikkelia. Levossa nesteen sisäistä kitkaa ei ole, joten sisäisistä voimista vain nesteen oman painon aiheuttama paine vaikuttaa nestepartikkeliin. Ulkoisista voimista siihen vaikuttaa vain Maan painovoima, jos Kuun ja Auringon pienet vetovoimat jätetään huomiotta.
Tarkasteltava nestepartikkeli on pieni kuutio, jonka sivut ovat Δx, Δy ja Δz. Siihen vaikuttava painevoima saadaan kertomalla pintaan kohdistuva paine pinnan alalla, tässä tapauksessa kuution sivujen aloilla (ΔxΔy, ΔyΔz ja niin edelleen).
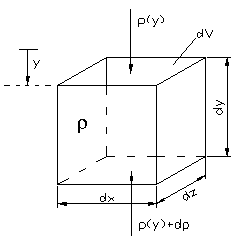
Jotta nestepartikkeli olisi levossa, tulee siihen vaikuttavien voimien kumota toisensa kaikkien koordinaattiakselien suunnissa. Tarkastellaan tilannetta aluksi x-suunnassa. Siinä
- .
Tässä on paineen muutos, kun liikutaan x-akselia pitkin matkan Δx verran. Muutosta on arvioitu Taylorin kaavalla, toista tai korkeampaa kertalukua olevat termit on jätetty pois.
Kaava sievenee muotoon . Jaetaan Δx:llä, jolloin saadaan . (Täsmällisemmin: aiemmin sivuutetut korkeamman kertaluvun termit katoavat Δx:llä jaettaessa, kun annetaan Δx:n lähestyä nollaa. Näin voidaan tehdä, kun neste oletetaan kontinuumiksi eli jatkuvasti jakautuneeksi.)
Kun täsmälleen sama tarkastelu suoritetaan y-akselin suunnassa, saadaan . Tästä nähdään, että hydrostaattisessa tilanteessa vaakasuuntaisia paine-eroja ei ole. Samalla syvyydellä nesteessä vallitsee sama paine.
z-suunnassa tilanne muuttuu, koska partikkeliin vaikuttaa myös sen paino alaspäin. Paino saadaan kertomalla partikkelin massa (tiheys kertaa tilavuus) painovoimakiihtyvyydellä g. Liikeyhtälöksi tulee
- .
Kun -termit kumoutuvat ja yhtälö jaetaan partikkelin tilavuudella ΔxΔyΔz, saadaan
- eli .
Koska paine muuttuu vain z-akselin suunnassa eikä riipu ajasta, saadaan hydrostatiikan perusyhtälö
- .
Hydrostatiikan perusyhtälö kertoo paineen muutoksen, kun liikutaan z-akselin suunnassa (nesteessä syvemmälle tai kohti pintaa). Jos sitä integroidaan nesteen pinnalta (z = 0) tarkastelusyvyydelle z, saadaan hydrostaattisen paineen yhtälö p = p0 - g ρ z.
Noste[muokkaa | muokkaa wikitekstiä]
- Pääartikkeli: Noste
Nesteeseen upotettavaan kiinteään kappaleeseen vaikuttaa sen syrjäyttämän vesimäärän painon suuruinen noste ylöspäin. Tämä periaate tunnetaan Arkhimedeen lakina. Noste johtuu siitä, että hydrostaattinen paine kappaleen yläpinnalla on pienempi kuin sen alapinnalla, ja sen vaikutuspiste on kappaleen geometrinen keskipiste. Mikäli kelluva kappale on vain osittain pinnan alapuolella, noste vaikuttaa uppoaman eli pinnan alla olevan kappaleen osan geometriseen keskipisteeseen. Painovoima puolestaan vaikuttaa kappaleen painopisteeseen.
Kelluvien kappaleiden kuten laivan noste tasapainottaa painovoiman. Jos laivaan lastataan lisää tavaraa, se syrjäyttää enemmän vettä ja siten myös noste on suurempi.
Stabiliteetti[muokkaa | muokkaa wikitekstiä]
Kelluva kappale on vakaa eli stabiili, jos se palaa tasapainoasemaansa, vaikka sitä poikkeutettaisiin hieman. Kelluvat kappaleet ovat yleensä vertikaalisesti stabiileja: jos kappaletta painetaan hiukan alaspäin, noste palauttaa kappaleen tasapainoon.
Epävakaa on esimerkiksi sellainen tila, jossa kokonaan upoksissa olevan kappaleen massakeskipiste on geometrisen keskipisteen yläpuolella. Jos kappale poikkeutetaan tasapainotilasta, se pyörähtää ympäri. Jos kelluva kappale sitä vastoin on osittain pinnan yläpuolella, voi tila olla stabiili vaikka geometrinen keskipiste olisikin massakeskipistettä alempana, sillä kappaletta poikkeutettaessa uppoaman geometrinen keskipiste (nosteen vaikutuspiste) muuttuu. Syntyy palauttava momentti, joka oikaisee kellunnan.









