Fermienergia

Fermienergia on kvanttimekaaninen käsite, jolla tarkoitetaan elektronisysteemin ylintä miehitettyä energiatilaa absoluuttisessa nollapisteessä. Fermienergia koskee elektronien lisäksi kaikkia fermioneja.
Fermienergia voidaan ymmärtää teoreettisella ajatuksella, jossa systeemiin, alimmalta energiatilalta lähtien, lisätään yksi kerrallaan partikkeleja. Kun kaikki partikkelit on laitettu systeemiin, fermienergia on ylimmän miehitetyn tilan energia. Käytännössä tämä tarkoittaa, että vaikka aine olisi jäähdytetty absoluuttiseen nollapisteeseen, elektronit liikkuvat silti ja nopeimmalla elektronilla on kineettinen energia, joka vastaa fermienergiaa. Tätä nopeutta kutsutaan ferminopeudeksi.
Johdanto[muokkaa | muokkaa wikitekstiä]
Kvanttimekaniikassa tiettyä joukkoa partikkeleista, jotka noudattavat Paulin kieltosääntöä, kutsutaan fermioneiksi. Tällaisia fermioneja ovat mm. leptonit (esim. elektroni), kaikki kvarkit ja hadroneista kaikki baryonit ja antibaryonit (esim. protoni ja neutroni). Paulin kieltosäännön mukaan kaksi samanlaista fermionia – esimerkiksi elektronia – ei voi olla yhtä aikaa täsmälleen samassa kvanttitilassa. Tilat voidaan erottaa toisistaan kvanttiluvuilla(pääkvanttiluku n, sivukvanttiluku l, magneettinen kvanttiluku ml ja spinkvanttiluku ms). Jos esimerkiksi systeemi, jossa on useita fermioneja (esim. elektroneja metallissa) kahdella saman atomin elektronilla ei voi olla samaa neljän kvanttiluvun yhdistelmää.
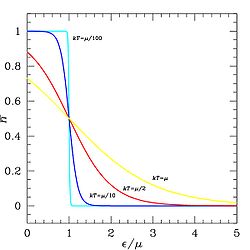
Koska elektronin spinkvanttiluku voi olla joko +1/2 tai −1/2, samalla tilalla voi Paulin kieltosäännön mukaan olla enintään kaksi elektronia. Elektronit, kuten kaikki muutkin fermionit noudattavat Fermi-Dirac statistiikkaa. Absoluuttisessa nollapisteessä vapaiden elektronien kaasun kaikki energiatasot on miehitetty Fermienergiaan asti. Lämpötilan kohotessa osa elektroneista siirtyy Fermipinnan alapuolelta sen yläpuolelle. Fermin-Diracin jakauma:
ilmoittaa todennäköisyyden, jolla tila E on miehitetty. Kemiallinen potentiaali on lämpötilasta riippuva suure. Absoluuttisessa nollapisteessä fermienergia ja kemiallinen potentiaali ovat yhtä suuret, eli . Suurilla energian arvoilla ja f(E) lähestyy Maxwellin–Boltzmannin jakaumaa:
- .
Vapaan elektronin energiatilat[muokkaa | muokkaa wikitekstiä]
Vapaaelektroniapproksimaatiossa ei oteta huomioon elektronien keskinäisiä eikä runkoionien ja elektronien välisiä vuorovaikutuksia. Systeemin potentiaalienergia U = 0 ja vapaan elektronikaasun koko energia on kineettistä energiaa.
Elektronit 1-ulotteisessa liikkeessä[muokkaa | muokkaa wikitekstiä]
Tarkastellaan 1-ulotteista ääretöntä potentiaalikaivoa, jonka pituus on L. Tämä on standardimalli kvanttimekaniikassa ja sen ratkaisu yhdelle partikkelille tunnetaan. Koska U = 0, saadaan energiatilat ratkaisemalla ajasta riippumaton Schrödingerin yhtälö:
- ,
kun huomioidaan reunaehdot , saadaan ratkaisuksi
aaltofunktio:
energia: .
Tarkastellaan N:n elektronin systeemiä, jonka energiatasot on miehitetty kvanttiluvusta n =1 tasoon nf asti ja kaikki ylemmät energiatilat ovat tyhjiä. Koska kaksi elektronia voi olla samalla tasolla on ylimmän miehitetyn tilan kvanttiluku tällöin N/2. Koska Fermienergia määritellään perustilassa olevan elektronisysteemin ylimmän täytetyn tason energian mukaan, saadaan Fermienergiaksi tällöin:
- .
Elektronit 3-ulotteisessa liikkeessä[muokkaa | muokkaa wikitekstiä]
Kolmiulotteinen tapaus voidaan ajatella kuutiona, jonka sivunpituus on L ja tilavuus V = L^3. Tämä malli osoittautuu erittäin hyväksi approksimaatioksi kuvaamaan elektroneja metallissa. Kun U = 0, voidaan Schrödingerin yhtälö kirjoittaa muotoon:
- ,
jonka ratkaisuna (ei esitetä tässä) saadaan kineettisen energian arvot:
- ,
missä , j = x, y, z ja ni = 0, 1, 2,… ja .
Lämpötilassa T = 0 elektronit täyttävät alimpia energioita edustavat k-tilat tiettyyn energia-arvoon (Fermienergia) asti. N:n elektronin systeemissä, jonka tasot on miehitetty aaltovektoritilaan kf asti, Fermienergia on
- .
Koska energia E on aaltovektorin itseisarvon funktio, ovat kaikki elektronikaasumallin tasaenergiapinnat pallopintoja. Ulointa miehitettyä tasaenergiapintaa nimitetään Fermi-pinnaksi. Pallossa jonka säde on kf ja pallon tilavuus , täyttää ehdon:
- ,
missä kerroin 2 johtuu spinistä (kaksi elektronia mahtuu samalle tilalle) ja tekijä on 1/8 pallon tilavuudesta, koska huomioidaan vain positiiviset kvanttilukujen arvot.
Josta seuraa Fermipallon säde k-avaruudessa:
- ,
jolloin Fermienergia voidaan kirjoittaa muodossa:

.
Edelleen voidaan määritellä ns. Ferminopeus, joka on siis elektronien nopeus Fermipinnalla:
- .
Fermilämpötila, joka on siis lämpötila Fermipinnalla voidaan määritellä yhtälöstä:
- .
Yllä mainitut suureet on hyvin määritelty vain jos Fermipinta on pallopinta.
Käyttö[muokkaa | muokkaa wikitekstiä]
Fermi-energia on tärkeä käsite tiiviin aineen fysiikassa, koska fermionisysteemin havaittavat ominaisuudet riippuvat kyseisen systeemin käytöksestä Fermi-energian läheisyydessä. Kiinteissä aineissa Fermi-energia on yleensä useita elektronivoltteja, kun huoneenlämpötila on noin 25 millielektronivolttia. Täten erityisesti metallien ominaisuudet voidaan selittää lähellä Fermi-energiaa sijaitsevia termisiä eksitaatioita tutkimalla.
Katso myös[muokkaa | muokkaa wikitekstiä]
Lähteet[muokkaa | muokkaa wikitekstiä]
- Lähteenkorva, E. E.: Materiaalifysiikka, s. 180, 253. Jyväskylä: Suomen Fyysikkoseura r.y., 1993. ISBN 951-96117-7-0.
- Paakkari, T.: Termofysiikka, s. 124. Helsinki: Limes ry, 1997. ISBN 951-745-174-1.
- 41 Kiinteän aineen sähkönjohtavuus (pdf) eh.net. Arkistoitu 28.9.2013. Viitattu 3.6.2009.
- Fermi level and Fermi function hyperphysics.phy-astr.gsu.edu. Viitattu 3.6.2009. (englanniksi)






















