PERT
PERT (Program Evaluation and Review Technique) on menetelmä, jonka avulla voidaan suunnitella ja aikatauluttaa kompleksisen projektin kulkua olosuhteissa, joissa ei ole mahdollista etukäteen arvioida tarkkaan yksittäisten projektin tehtävien viemää aikaa.
Yleistä[muokkaa | muokkaa wikitekstiä]
PERT-menetelmä kehitettiin alun perin helpottamaan suurten ja monimutkaisten hankkeiden projektinhallintaa. Se pyrkii ottamaan huomioon ja tekemään näkyväksi sen epävarmuuden, joka projektien aikataulujen laadintaan tyypillisesti liittyy. Tiettävästi menetelmää käytettiin menestyksekkäästi Yhdysvaltain laivaston Polaris-ohjuksen kehittäneessä Fleet Ballistic Missiles Program -ohjelmassa.
PERT-menetelmän käyttö edellyttää sitä, että projektien eri tehtävistä voidaan piirtää vuokaavio, ns. toimintaverkko, jossa projektin eteneminen ja eri tehtävien väliset riippuvuudet tulevat esiin. Myös eri tehtävien vaatimasta ajasta on pystyttävä antamaan jonkinlaiset skaala-arviot. PERT-menetelmä perustuu siihen, että tehtävien kestoaikojen vaihteluvälistä voidaan tehdä tilastollisia analyysejä.
Kun projektin toivottu valmistumisajankohta on tiedossa, voidaan PERT-menetelmällä laskea, mikä on todennäköisyys sille, että projekti saadaan valmiiksi juuri siihen ajankohtaan mennessä. Myös projektin seurantaa helpottamaan asetettujen välitavoitteiden, eli virstanpylväiden (ns. milestone), toivottujen päivämäärien kohdalla voidaan tehdä vastaavat todennäköisyysalaskelmat.
PERT-menetelmän vahvuutena on pidetty sitä, että se korostaa aikatauluarvioiden epävarmuutta, kertoen vain ajakohdan, johon mennessä jonkin projektin vaihteen voi odottaa valmistuvan. PERT-kaavio tuo myös hyvin esiin projektin ns. kriittisen polun, ja kiinnittää huomion niihin tehtäviin, joilla on suurin vaikutus projektin riskiin epäonnistua.
PERT-menetelmä käytännössä[muokkaa | muokkaa wikitekstiä]
Projektin toimintaverkon piirtäminen[muokkaa | muokkaa wikitekstiä]
PERT-analyysiin ensimmäinen vaihe on PERT-kaavion piirtäminen. PERT-kaavio on toimintaverkko, joka kuvaa projektin etenemisjärjestystä, ja eri tehtävien suoritusjärjestys ja keskinäiset riippuvuudet tulevat siitä esille. Suoritettavia tehtäviä kuvataan nuolilla, jotka johtavat yhdestä projektivaiheesta toiseen. Kaaviossa tehtävät voidaan yksilöitä vaikkapa kirjaimilla (tehtävä A, tehtävä B, jne). Projektivaiheita taas voidaan kuvata laatikoilla, joita nuolet yhdistävät.
Tässä pienessä esimerkissä arvioimme seuraavanlaista, kuvitteellista ohjelmistoprojektia, jossa projektihenkilökunnan pitää suorittaa seuraavat tehtävät:
* Tehtävä A: ohjelmamoduulin X suunnittelu * Tehtävä B: ohjelmamoduulin X toteutus (tehtävän A jälkeen) * Tehtävä C: ohjelmamoduulin Y suunnittelu * Tehtävä D: ohjelmamoduulin Y toteutus (tehtävän C jälkeen) * Tehtävä E: ohjelmamoduulien integrointi (tehtävien B ja D jälkeen) * Tehtävä F: testauksen suunnittelu * Tehtävä G: integrointitestien toteutus (tehtävän F jälkeen) * Tehtävä H: integrointitestaus (tehtävien E ja G jälkeen) * Tehtävä I: tyyppihyväksyntätestien toteutus (tehtävän F jälkeen) * Tehtävä J: tyyppihyväksyntätestaus (tehtävien H ja I jälkeen)
Näillä tiedoilla voimme piirtää tilanteesta toimintaverkon (ks. Kuva 1). Kuvassa projektin tehtäviä kuvaaviin nuoliin on merkitty ko. tehtävän tunnistekirjain. Projektin vaiheita kuvaaviin laatikkohin on merkitty vasempaa yläkulmaan ko. vaiheen tunnistenumero. Näin esimerkiksi nuoli C kuvaa heti projekti alussa aloitettavaa tehtävää "ohjelmamoduulin Y suunnittelu". Sen suorittamisen jälkeen ollaan vaiheessa 3, jolloin toteutussuunnitelma moduulille Y on siis valmis.

- Vaihe 1 on projektin tämän tarkasteluvaiheen aloituspiste, ns. viikko 0, ja yksinkertaisuuden vuoksi oletamme, että tässä vaiheessa projektissa on jo tarjolla kaikki tarvittavat systeemitason suunnitelmat yms.
- Vaiheessa 6 on tarkoitus toimittaa raaka-versio tuotteesta alihankkijalle integrointitestattavaksi. Toimitus on sovittu 60 työpäivän (l. noin 3 kuukautta, kun kuukaudessa on laskennallisesti 21,5 työpäivää) päähän projektin aloituksesta.
- Koko projekti on tarkoitus saada valmiiksi vaiheessa 8, jolloin aikaa aloituksesta on kulunut 80 työpäivää, eli noin 3 työkuukautta ja 3 viikkoa. Kuvassa projektin vaiheita kuvaaviin laatikkohin on oikeaan yläkulmaan merkitty vaiheen tavoiteltu ajankohta (tässä: työpäivinä).
Huomaa, että mikäli tiettyyn projektivaiheeseen voidaan saapua useita eri nuolireittejä pitkin, kaavio tulee ymmärtää siten, että kaikkien nuolten kuvaamien tehtävien tulee olla valmiita, ennen kuin ko. vaiheeseen asti on todella päästy. Esimerkiksi vaiheeseen 6 voidaan saapua kolmea eri reitti pitkin: A+B+E, C+D+E tai F+G. Jotta vaihe 6 olisi saavutettu, pitää siis kaikkien tehtävien A-G olla ensin suoritettu. Toimintaverkko kuvaa näin reaalimaailman tilannetta: jotta vaiheen 6 jälkeen voitaisiin suorittaa suunniteltu ohjelmiston integrointitestaus (tehtävä H), pitää testattavan ohjelmiston toki olla ensin suunniteltu, toteutettu ja integroitu, sekä testauksessa ajettavaksi tarkoitetun ingegrointitestisetin suunniteltu ja toteutettu.
Tehtävien keston ennustaminen[muokkaa | muokkaa wikitekstiä]
Seuraavaksi pitää arvioida, kuinka kauan aikaa kunkin yksittäisen tehtävän suorittaminen voi viedä. Optimistinen aika-arvio to on arvaus siitä, kuinka nopeasti tehtävän voisi saada suoritetuksi, jos kaikki mahdollinen sujuisi hyvin – pois lukien suoranaiset ihmeet. Normaali aika-arvio tn on arvio siitä, kuinka kauan aikaa vastaavanlaisten tehtävän tekeminen yleensä vie. Pessimistinen aika-arvio tp taas näkemys tehtävän kestosta silloin, jos kaikki ko. tehtävään liittyvät, suhteellisen todennäköiset riskit toteutuvat.
Ennuste projektin tehtävän todellisesta kestosta, te, lasketaan seuraavalla kaavalla, jossa normaaliarvio saa isomman painotuksen kuin muut arviot.
Oletamme nyt, että kuvitteellisen esimerkkiprojektimme henkilökunta on saanut tutustua projektin tuleviin tehtäviin, ja antanut parhaat arvionsa tehtävien kestoista, harkiten tarvittua aikaa niin parhaassa, tavallisessa kuin pahimmassakin tilanteessa. Ao. taulukossa on esitetty eri tehtäville arvioidut kestot, sekä niistä ym. kaavalla laskettu tehtävän ennustekesto.
| Tehtävä | Edeltävät tehtävät | Annettu aika-arvio | Laskettu ennuste (te) | ||
|---|---|---|---|---|---|
| Optimistinen (to) | Normaali (tn) | Pessimistinen (tp) | |||
| A | — | 14 | 20 | 22 | 19,33 |
| B | A | 19 | 25 | 28 | 24,5 |
| C | — | 13 | 15 | 18 | 15,17 |
| D | C | 25 | 30 | 38 | 30,5 |
| E | A...D | 4 | 5 | 11 | 5,83 |
| F | — | 17 | 25 | 27 | 24 |
| G | F | 14 | 20 | 26 | 20 |
| H | A...G | 8 | 10 | 16 | 10,67 |
| I | F | 30 | 35 | 39 | 34,83 |
| J | A...I | 12 | 15 | 20 | 15,33 |
Kun yo. taulukosta saatavat eri tehtävien ennustekestot sijoitetaan PERT-kaavioon (ks Kuva 2), voimme sen jälkeen laskea, kuinka kauan projektivaiheeseen pääseminen voi pisimmillään kestää. Kaaviossa on merkitty kunkin tehtävän tunnistekirjaimen alle ko. tehtävän ennustettu kesto, te.

Tehtävien ennustettuja kestoja yhteen laskemalla päätellä koko suorituspolun kesto, tiettyyn vaiheeseen saakka:
- Vaihe 1: aloituspiste, kesto = 0.
- Vaihe 2: vain yksi reitti, kesto = tehtävän A:n te = 19,33.
- Vaihe 3: vain yksi reitti, kesto = tehtävän C:n te = 15,17.
- Vaihe 4: kaksi vaihtoehtoista reittiä, joista suurempi kesto otetaan käyttöön:
- Suorituspolku A+B = 19,33 + 24,5 = 43,83.
- Suorituspolku C+D = 15,17 + 30,5 = 45,67.
- Vaihe 5: vain yksi reitti, kesto = tehtävän F:n te = 24.
- Vaihe 6: kaksi vaihtoehtoista reittiä, joista suurempi kesto otetaan käyttöön:
- Suorituspolku te(vaihe 4)+E = 45,67 + 5,83 = 51,5.
- Suorituspolku te(vaihe 5)+G = 24 + 20 = 44.
- Vaihe 7: kaksi vaihtoehtoista reittiä, joista suurempi kesto otetaan käyttöön:
- Suorituspolku te(vaihe 5)+I = 24 + 34,83 = 58,83.
- Suorituspolku te(vaihe 6)+H = 51,5 + 10,67 = 62,17.
- Vaihe 8: vain yksi reitti, kesto = te(vaihe 7)+J = 62.17 + 15,33 = 77,5.
Eri suoritusreittien pisimät kestot merkitään PERT-kaaviossa projektin ko. vaihetta kuvaavan laatikon vasempaan alanurkkaan (ks. Kuva 3).

Kaaviosta saadaan nyt hyvä käsitys siitä, miten projekti todennäköisesti etenee. Voidaan huomata, että pisin suoritusreitti kulkee tehtävien C ja D kautta – ohjelmamoduulin Y suunnittelu ja toteutus ovat siis projektin kannalta kriittisiä tehtäviä. Projektin kriittinen polku on merkitty kaavioon punaisin tehtävänuolin.
Kaaviosta voidaan myös huomata, että välivaiheen 6 saavuttaminen aikataulussa näyttää varsin mahdolliselta, koska te(vaihe 6) on vain 51,5 päivää, mutta vaiheen varsinaisena tavoitteena on vasta 60. päivä. Koko projektin suorittaminen aikataulussa näyttää sekin mahdolliselta, vaikkakin välitavoitetta pienemmälä marginaalilla, koska te(vaihe 8) on 77.5 päivää, ja koko projektin olisi tarkoitus valmistua 80. päivään mennessä.
Keskihajonnan laskeminen[muokkaa | muokkaa wikitekstiä]
Tehtäviin liittyvä keskihajonta[muokkaa | muokkaa wikitekstiä]
Tietyn tehtävän kestoarvioiden keskihajontaa (merk. s) voidaan pitää jonkinlaisena mittarina siitä, kuinka epävarmaa ko. tehtävän suorittamisen onnistuminen on. Mitä kauempana tehtävän optimistinen ja pessimistinen aika-arvio ovat toisistaan, sitä epäluottavampi on myös koko arvio siitä, kuinka paljon aikaa tehtävän suorittamiseen voi ylipäätään kulua. Tehtävien kestoarvoiden keskihajonta voidaan laskea seuraavalla kaavalla:
Ao. taulukossa on esitetty eri tehtävistä annetuille aika-arvioille laskettu keskihajonta:
| Tehtävä | Edeltävät tehtävät | Annettu aika-arvio | Keskihajonta (s) | |
|---|---|---|---|---|
| Optimistinen (to) | Pessimistinen (tp) | |||
| A | — | 14 | 22 | 1.33 |
| B | A | 19 | 28 | 1,5 |
| C | — | 13 | 18 | 0,83 |
| D | C | 25 | 38 | 2,17 |
| E | A...D | 4 | 11 | 1,17 |
| F | — | 17 | 27 | 1,67 |
| G | F | 14 | 26 | 2 |
| H | A...G | 8 | 16 | 1,33 |
| I | F | 30 | 39 | 1,5 |
| J | A...I | 12 | 20 | 1,33 |
PERT-kaavioon merkitään nyt eri tehtävien kestoille lasketut keskihajonta-arvot (ks. Kuva 4). Saatuja keskihajonta-lukuja tarvitaan jatkossa projektin aikataulussa pysymisen todennäköisyyden laskemiseen.

Vaiheisiin liittyvä keskihajonta[muokkaa | muokkaa wikitekstiä]
Projektin tietyn vaiheen keskihajonta riippuu vaiheeseen tuovan suorituspolkun keskihajonnasta. Tietyn suorituspolun tehtävien keskihajonta-arvoja ei voi laskea yhteen suoraan, vaan ensin on laskettava polun eri tehtävien keskihajontojen neliöt yhteen, ja sitten otettava tästä summasta neliöjuuri. Esimerkiksi suorituspolun (A+B) keskihajonta lasketaan siis kaavalla
Mikäli suorituspolkuja tiettyyn vaiheeseen pääsemiseksi on useita, katsotaan suorituspolkujen suurin keskihajontaluku ko. vaiheen keskihajonta-arvoksi. Tässä esimerkki laskukaavasta, projektin vaiheeseen 4 liittyen:
vaihe4
Vaiheeseen 4 liittyvä keskihajonta-arvo on siis tässä suurin niistä keskihajontaluvuista, jotka ovat laskettavissa ko. vaiheeseen liittyvistä suorituspoluista (A+B) tai (C+D).
vaihe4
PERT-kaavioon merkitään nyt viimeisessä vaiheessa kullekin projektivaiheelle ym. menetelmillä lasketut keskihajonta-arvot. Luku merkitään kaaviossa projektivaihetta kuvaavan laatikon oikeaan alanurkaan (ks. Kuva 5).
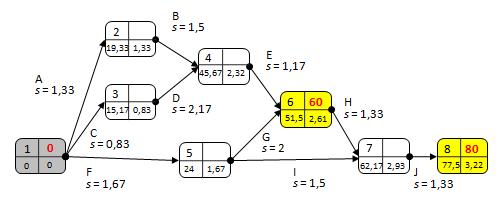
Todennäköisyyksien arviointi[muokkaa | muokkaa wikitekstiä]
Projektin tietyn vaiheen aikataulussa saavuttamisen todennäköisyytta voidaan nyt arvioida ko. vaiheen tunnusluvulla z. Tunnusluku lasketaan kaavalla:
jossa T on tarkasteltavalle vaiheelle asetettu tavoiteaika, te vaiheen ennustettu saavuttamisaika, ja s ko. vaiheelle laskettu keskihajonta-arvo. Näin voidaan laskea z-arvot niille kahdelle projektivaiheelle, joille olemma asettaneet tavoitearvon:
- Vaihe 6, eli ohjelmiston toimittaminen ulkopuolisella alihankkijalle integrointitestattavaksi.
Tavoiteaika T = 60 päivää, ennustettu aika te = 51,5 päivää, ja vaiheen keskihajonta-arvo s = 2,61.
Nyt .
- Vaihe 8, eli projektin valmistumispäivä. Tavoiteaika T = 80 päivää, ennustettu aika te = 77,5 päivää, ja vaiheen keskihajonta-arvo s = 3,22.
Nyt .
Ym. z-arvot voidaan nyt muuttaa todennäköisyyksiksi standardinormaalijakauman avulla (ks. Kuva 6). Kuvassa näkyvä vihreä funktio on standardinormaalijakauman kertymäfunktio (eli siten, että ja ). Tarkempi taulukko funktion arvoista ("Approximate values of the standard normal distribution function") on saatavilla esim. osoitteessa http://www.fmi.uni-sofia.bg/vesta/Virtual_Labs/tables/tables1.html (Arkistoitu – Internet Archive).

- Kuvaajasta voidaan lukea, että standardinormaalijakauman kertymäfunktion arvo pisteessä x=3,26 on 0,9994.
- Tämä on tulkittavissa siten, että todennäköisyys sille, että vaihe 6 saavutetaan suunnitellussa aikataulussa kuvatun kaltaisella projektisuunnitelmalla, on n. 100% – eli siis varmaa.
- Edelleen kuvaajasta voidaan lukea, että standardinormaalijakauman kertymäfunktion arvo pisteessä x=0,77 on 0,7794.
- Tämä on tulkittavissa siten, että todennäköisyys sille, että koko projekti saada valmiiksi suunnitellussa aikataulussa on n. 78%.
- Projekti siis lipsuu 22% todennäköisyydellä eteenpäin aikataulussaan.
Koko projektin onnistumisen mahdollisuuksia voisi siis ehkä yrittää parantaa, esim. aikaistamalla vaiheen 6 suunniteltua tavoitepäivää, jolloin integrointitestaus (tehtävä H) pääsisi alkamaan aikaisemmin.
- Voisiko vaihe 6 valmistua jo esim. 55 päivään mennessä, eli noin viikon aiottua aikaisemmin?
- Voimme laskea, että T:n arvolla 55, vaiheen 6 standardipoikkeama-arvoksi saataisin ym. kaavalla 1,34. Kuvaajasta voidaan lukea, että standardinormaalijakauman kertymäfunktion arvo pisteessä x=1,34 on 0,9082.
- Tämä on tulkittavissa siten, että todennäköisyys sille, että vaihe 6 saavutetaan 55. päivään mennessä, on yhä n. 91%. Projektisuunnitelman muutamista on siis syytä harkita.
Kritiikkiä[muokkaa | muokkaa wikitekstiä]
PERT-menetelmässä oletetaan, että projektin tehtävien määrä on riittävän suuri ja ne ovat toisistaan tilastollisesti riippumattomia. Tällöin myös tehtävien ja koko projektin laskennallinen kokonaisaika ja tehtävien suoritusajoissa esiintyvä vaihtelu ovat normaalisti jakautuneita, ja todennäköisyyksien arviointi standardinormaalijakauman avulla on mahdollista ja järkevää.
Pienissä projekteissa (kuten sivulla olleessa kuvitteellisessa ohjelmistoprojektissa), joissa on vain vähän tehtäviä, ym. olettamus ei aina pidä paikkaansa, ja PERT-menetelmällä saadut tulokset eivät ole luotettavia.
Lähteet[muokkaa | muokkaa wikitekstiä]
- Bob Hughes, Mike Cotterell: Sotfware Project Management. 4th ed. McGraw-Hill, 2006. ISBN 0-07-710989-9.
- Heli Helminen: Työmääräarviointi ja aikataulusuunnittelu IT-projekteissa. Pro gradu -tutkielma. Tampereen yliopisto, tietojenkäsittelytieteiden laitos, 2008. Teoksen verkkoversio (viitattu 30.11.2011). [vanhentunut linkki].











