Derivaatta

Derivaatta tarkoittaa matematiikassa reaaliarvoja saavan funktion herkkyyttä muutokselle yhden sen riippumattoman muuttujansa suhteen. Derivaatta on matemaattisen analyysin peruskäsitteitä. Se johdetaan funktion tietyn välin keskimääräisestä muutosnopeudesta, jonka arvosta määritetään raja-arvon avulla muutosnopeus yhdessä kohtaa. Sanaa derivaatta käytetään Suomessa sekä funktion derivaatan arvon että sen derivaattafunktion synonyyminä.

Jos rajoitutaan yhden muuttujan funktioihin, voidaan muutosnopeuden keskiarvoa kuvata funktion kuvaajan keskimääräiseksi jyrkkyydeksi. Sitä havainnollistetaan esimerkiksi Suomen lukioiden matematiikan oppimäärissä kuvaajan sekantilla (keskimääräinen muutosnopeus), jonka kulmakerroin on kyseisellä välillä funktion jyrkkyyksien likiarvo. Mitä pienempi on sekantin rajaama väli, sitä paremmin sen jyrkkyys vastaa funktion kuvaajan jyrkkyyksiä kyseisellä välillä. Lopulta, kun väliä pienennetään raja-arvon avulla pisteeksi, saadaan derivaatta (muutosnopeus yhdessä kohdassa). Sitä havainnollisetaan yleensä tangentilla, jonka kulmakerroin on derivaatan arvon suuruinen.

Yhden muuttujan derivaatta voidaan yleistää usean muuttuja funktioille, jossa sitä kutsutaan funktion differentiaaliksi. Differentiaali on funktion kokonaismuutoksen lineaarinen osa, joka esitetään Jacobin matriisin avulla.

Yhden reaalimuuttujan funktiot

Sekantin asennon kääntyminen tangentiksi.

Määritelmä kahden kohdan avulla

Yhden reaalimuuttujan funktion $f(x)$ derivaatan $f'(x)$ formaalinen määritelmä käyttää aina hyväkseen sen muutosnopeuden raja-arvoa. Seuraavassa funktion muutosnopeutta ilmaistaan sen erotusosamäärällä käyttäen valitun välin päätepisteitä $x_{0}$ ja $x$

${\frac {\text{funktion f arvon muutos}}{\text{muuttujan x arvon muutos}}}={\frac {\Delta f}{\Delta x}}={\frac {f(x)-f(x_{0})}{x-x_{0}}}.$

Merkinnällä $\Delta a$ tarkoitetaan suureen $a$ arvojen muutosta tai erotusta $a_{1}-a_{2}$. Välin $[x_{0},x]$ jälkimmäistä päätepistettä $x$ siirretään lähemmäksi välin ensimmäistä päätepistettä $x_{0}$. Tämä merkitään raja-arvon arvolla

$\lim _{x\to x_{0}}{\frac {f(x)-f(x_{0})}{x-x_{0}}}.$

Tällöin voidaan sanoa (jos raja-arvo on olemassa), että funktiolla $f(x)$ on derivaatan arvo kohdassa $x_{0}$, joka merkitään tavallisesti $f'(x_{0})$.

Määritelmä välin pituuden avulla

Erotusosamäärä ja sekantti.

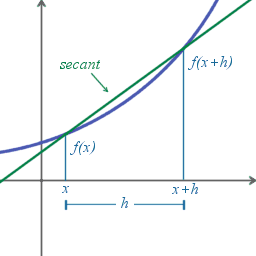
Toisessa yleisessä määritelmässä erotusosamäärä muodostetaan pisteiden $x_{0}$ ja $x=x_{0}+h$ avulla, missä luku $h=x-x_{0}$ on pisteiden välinen etäisyys. Sijoittamalla tämä erotusosamäärään saadaan

${\frac {\Delta f}{\Delta x}}={\frac {f(x_{0}+h)-f(x_{0})}{(x_{0}+h)-x_{0}}}={\frac {f(x_{0}+h)-f(x_{0})}{h}}.$

Nyt väliä $[x_{0},x]=[x_{0},x_{0}+h]$ voidaan raja-arvossa pienentää pienentämällä lukua $h$, jolloin saadaan (mikäli raja-arvo on olemassa) derivaatan arvo pisteessä $x_{0}$

$f'(x_{0})=\lim _{h\to 0}{\frac {f(x_{0}+h)-f(x_{0})}{h}}.$

Derivaatan olemassaolo

Derivaatta on olemassa pisteessä $x_{0}$, mikäli erotusosamäärän raja-arvo on äärellinen ja se voidaan määrittää yksikäsitteisesti. Käyttämällä hyväksi toispuoleisen derivaatan käsitteitä, voidaan derivaatan olemassaolo ilmaista niin, että sekä vasemmanpuoleinen että oikeanpuoleinen derivaatta tulee olla olemassa ja niiden arvot tulisi olla yhtä suuret.

Vaikeasti käyttäytyvillä funktioilla ei riitä erotusosamäärän raja-arvon intuitiivinen sievennys, vaan tarvitaan täsmällisempi matemaattinen määritelmä. Sellainen on esimerkiksi

$\forall {\epsilon >0}\,\exists {\delta >0}:|x-x_{0}|<\delta \Rightarrow \left|{f(x)-f(x_{0}) \over x-x_{0}}-f'(x_{0})\right|<\epsilon \,$.

Toisin sanoen kaikille ehdotetuille luvuille $\epsilon >0\,$ löytyy siitä riippuva luku $\delta >0\,$ siten, että erotusosamäärän arvot ovat alle $\epsilon \,$:in päässä raja-arvosta eli derivaatan arvosta, kun muuttujan arvot ovat alle $\delta \,$:n päässä lähestyttävästä arvosta. Mikäli aina lukua $\epsilon \,$ pienennettäessä, löytyy edellistä pienempi $\delta \,$, voidaan pitää osoitettuna, että raja-arvo tulee löytymään.

Yhden muuttujan derivaattafunktio

Derivaattafunktio tarkoittaa sellaista lauseketta, jolla voi laskea funktion derivaatan arvon kyseisessä kohdassa ilman raja-arvon määritystä. Tällaisen funktion määrittämistä kutsutaan derivoimiseksi. Derivointifunktiota kutsutaan yleisesti myös derivaataksi. Derivaattafunktion määrittelyjoukko voi olla sama kuin funktion määrittelyjoukko, mutta toisinaan se on suppeampi väli.

Määritetään funktion $f(x)$ derivaattafunktio missä funktion määrittelyjoukon pisteessä $x$ hyvänsä. Niissä pisteissä, missä raja-arvo on määritelty, saadaan derivaattafunktioksi $f'(x)$ (käytetään toista määritelmää)

$f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}.$

Tämän derivaattafunktion määrittelyjoukko saadaan, kun raja-arvon kannalta määrittelemättömät kohdat jätetään funktion määrittelyjoukosta pois.

Esimerkiksi funktion $f(x)=x^{2}$ derivaattafunktio määritetään seuraavasti. Merkitään lausekkeet erotusosamäärään ja määritetään raja-arvo:

$f'(x)=\lim _{h\to 0}{\frac {(x+h)^{2}-x^{2}}{h}}=\lim _{h\to 0}{\frac {(x^{2}+2hx+h^{2})-x^{2}}{h}}=\lim _{h\to 0}{\frac {2hx+h^{2}}{h}}=\lim _{h\to 0}(2x+h)=2x+0=2x.$

Lausekkeella $f'(x)=2x$ voi helposti laskea funktion $f(x)=x^{2}$ derivaatan arvojailman, että raja-arvoa tarvitsee enää määrittää.

Tilanteita, jossa derivaatan arvoa ei voi funktion määrittelualueelta määrittää, liittyvät esimerkiksi funktion liian suureen jyrkkyyteen. Silloin funktion kuvaajalle piiretty tangentti on pystysuora, jolle ei ole määritelty kulmakerrointa. Jos derivaatta voidaan määrittä kaikissa muissa funktion määrittelyjoukon kohdissa, muodostuu tästä derivaattafunktion määrittelyjoukko. Laajin väli, missä derivaatta on mielekästä määrittää, on funktion oma määrittelyjoukko.

Derivaatta-operaattori ja muita merkintätapoja

Operaattoria, jolla funktion derivoinnin aikomus ilmaistaan, merkitään derivaatta-operaattorilla. Suomenkin lukiokoulutuksessa on yleisesti käytössä iso D-kirjain. Edellisen esimerkin derivointia merkitään sillä

$Dx^{2}=2x.$

Toinen yleinen merkintä "pilkku"-merkintä, jossa funktion dervivaattafunktiota merkitään

$f'=f'(x)\,.$

Siinä oletetaan, että lukija tuntee muuttujan, jonka suhteen derivointi suoritetaan. Tämän vuoksi sitä käytetään pääasiassa yhden muuttujan dervivoinnissa. Mikäli muuttujana on aika (merkitään t), kuten fysiikassa on yleistä, käytetään "piste"-merkintää

${\dot {f}}={\dot {f}}(t)\,.$

Useamman muuttujan funktioissa voidaan suorittaa derivointi yhdelle muuttujalle, joka tulee ilmoittaa lukijalle alaindeksinä tai uudella merkinnällä

$D_{x}f={\frac {df}{dx}}\,.$

Merkinnät $df$ ja $dx$ tarkoittavat suureiden $f\,$ ja $x\,$ differenssejä ja nimittäjästä $dx$ voidaan päätellä, minkä muuttujan suhteen derivointi suoritetaan.

Derivaatan arvo jossakin kohdassa $a\,$ merkitään vastaavasti $f'(a)\,$, $Df(a)\,$, $\left({\frac {df}{dx}}\right)_{x=a}$ tai ${\dot {f}}(a)\,.$

Moninkertaiset derivaatat

Kun funktion $f\,$:n derivaattafunktio on myös derivoituva, voidaan funktiota $f\,$ kutsutaan kahdesti derivoituvaksi. Kahdesti derivoitu funktio eli toinen derivaatta määritetään

$f''(x)=\lim _{h\to 0}{\frac {f'(x+h)-f'(x)}{h}}$

ja merkitään $f''\,$, $D^{2}f(x)\,$ tai ${\frac {d^{2}f}{dx^{2}}}$. Derivaattafunktioiden derivaattoja tarvitaan monissa sovelluksissa. Silloin voidaan yleistää, että jos $f\,$:n $(n-1)\,$:s derivaattafunktio on derivoituva, niin funktio on $n\,$ kertaa derivoituva, ja sen $n\,$:ttä derivaattaa merkitään $f^{(n)}\,$, $D^{n}f(x)\,$ tai ${\frac {d^{n}f}{dx^{n}}}\,$.

Jos funktion ($n\,$:s) derivaatta on olemassa ja jatkuva, niin funktion sanotaan olevan ($n\,$ kertaa) jatkuvasti derivoituva. Mikäli funktion $n\,$:s derivaattafunktio on olemassa ja jatkuva, sanotaan, että funktio on $C^{n}\,$-funktio. Jos funktio on äärettömän monta kertaa derivoituva ja sen jokainen derivaattafunktio on jatkuva, niin funktion sanotaan olevan $C^{\infty }\,$-funktio.^lähde?

Eräiden alkeisfunktioiden derivointia

Seuraavassa luettelossa on eräiden alkeisfunktioiden derivaattojen muistikaavoja. Siinä ei oteta kantaa funktion ja derivaatan määrittelyjoukkoihin.

Potenssin derivaatta	Trigonometristen funktioiden derivaatat	Arkusfunktioiden derivaatat
$Dx^{n}=nx^{n-1}\,$, missä $n\in \mathbb {Z}$	$D\sin x=\cos x\,$	$D\arcsin x={1 \over {\sqrt {1-x^{2}}}}\,$
$D{\sqrt {x}}={1 \over 2{\sqrt {x}}}\,$	$D\cos x=-\sin x\,$	$D\arccos x=-{1 \over {\sqrt {1-x^{2}}}}\,$
$D{\sqrt[{3}]{x}}={1 \over 3{\sqrt[{3}]{x^{2}}}}\,$	$D\tan x={1 \over \cos ^{2}x}=1+\tan ^{2}x\,$	$D\arctan x={1 \over 1+x^{2}}\,$
$D{\sqrt[{n}]{x}}={1 \over n{\sqrt[{n}]{x^{n-1}}}}\,$	$D\cot x=-{1 \over \sin ^{2}x}=-1-\cot ^{2}x\,$	$D\operatorname {arccot} x=-{1 \over 1+x^{2}}\,$
Eksponenttifunktion derivaatta	Hyperbolisten funktioiden derivaatat	Hyperbolisten käänteisfunktioiden derivaatat
$De^{x}=e^{x}\,$	$D\sinh x=\cosh x\,$	$D\ \operatorname {arsinh} \,x={1 \over {\sqrt {x^{2}+1}}}\,$
$Da^{x}=a^{x}\ln a\,$, missä $a>0\,$	$D\cosh x=\sinh x\,$	$D\ \operatorname {arcosh} \,x={1 \over {\sqrt {x^{2}-1}}}\,$
	$D\tanh x={\frac {1}{\cosh ^{2}x}}\,$	$D\ \operatorname {artanh} \,x={1 \over 1-x^{2}}\,$
Logaritmifunktioiden derivaatat
$D\ln |x|={1 \over x}\,$
$D\log _{a}|x|={1 \over x\ln a}\,$, missä $a>0\,$ ja $a\neq 1$

Potenssin derivaattafunktio voidaan määrittää derivaatan määritelmän mukaan

$Df(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}\,,$

jolloin potenssifunktiolle saadaan

$Dx^{n}=\lim _{h\to 0}{\frac {(x+h)^{n}-x^{n}}{h}}\,.$

Koska

$(x+h)^{n}=a_{0}x^{n}+a_{1}hx^{n-1}+a_{2}h^{2}x^{n-2}+a_{3}h^{3}x^{n-3}+...+a_{n-1}h^{n-1}x+h^{n}\,$,

missä $a_{i}$ vastaa kunkin termin binomikerrointa (erityisesti $a_{0}=1\,$ ja $a_{1}=n\,$), voidaan erotusosamäärä kirjoittaa

$Dx^{n}=\lim _{h\to 0}{\frac {({\cancel {x^{n}}}+nhx^{n-1}+a_{2}h^{2}x^{n-2}+a_{3}h^{3}x^{n-3}+...+a_{n-1}h^{n-1}x+h^{n})-{\cancel {x^{n}}}}{h}}\,$

$=\lim _{h\to 0}(nx^{n-1}+a_{2}hx^{n-2}+a_{3}h^{2}x^{n-3}+...+a_{n-1}h^{n-2}x+h^{n-1})\,$

$=nx^{n-1}+0+0+...+0+0\,$

$=nx^{n-1}\,.$

Tämän todistuksen ja summaussäännön perusteella voidaan helposti todistaa polynomifunktion $\sum _{k=0}^{n}a_{k}x^{k}$ derivaatta.

Yleisiä derivointisääntöjä

Mikäli funktio on alkeisfunktioiden yhdistelmä, kuten niiden summa, erotus, tulo, osamäärä tai yhdistelmä, voidaan niitä derivoida.seuraavien sääntöjen puitteissa.

Säännön nimi	Derivointisääntö
Vakion derivaatta	$Dc=0\,$, kun $c\,$ on vakio.
Vakion siirto	$Dcf(x)=cDf(x)\,$
Summan derivaatta	$D(f(x)+g(x))=Df(x)+Dg(x)\,$
Tulon derivaatta	$D(f(x)g(x))=g(x)Df(x)+f(x)Dg(x)\,$
Funktion potenssin derivaatta	$Df(x)^{n}=nf(x)^{n-1}f'(x)\,$
Osamäärän derivaatta	$D{\frac {f(x)}{g(x)}}={\frac {g(x)Df(x)-f(x)Dg(x)}{g(x)^{2}}}\,$
Yhdistetyn funktion derivaatta	$Dg(f(x))=g'(f(x))f'(x)\,$
Käänteisfunktion derivaatta	$(f^{-1})'(f(x))={1 \over f'(x)}\,$, jossa $f^{-1}\,$ on $f\,$:n käänteisfunktio.

Vakiofunktion $f(x)=c$ derivointi voidaan suorittaa määritelmän kautta seuraavasti:

$Dc=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}=\lim _{h\to 0}{\frac {c-c}{h}}=0.$

Yhden kompleksimuuttujan funktiot

Jos merkitään kompleksilukujen muuttujia $z=x+iy$, ja tietyssä alueessa G (sisältää luvun $z_{0}$) määriteltyä kompleksifunktiota $f(z)=u(x,y)+iv(x,y)$, pystytään joskus määrittämään funktion $f(z)$ derivaatta.

Holomorfinen funktio

Derivaatta on olemassa, mikäli $f(z)$ toteuttaa Cauchyn–Riemannin yhtälöt ja sen osittaisderivaatat ovat pisteen $z_{0}$ ympäristössä G jatkuvat. Tällaisia kompleksifunktioita kutsutaan holomorfisiksi funktioiksi. Silloin raja-arvo

$f'(z_{0})=\lim _{z\to z_{0}}{\frac {f(z)-f(z_{0})}{z-z_{0}}}$

voidaan määrittää yksikäsitteisesti.

Derivaatan olemassaolo toteaminen

Esimerkiksi toisen asteen kompleksifunktio voidaan kirjoittaa auki

$f(z)=z^{2}=(x+iy)^{2}=x^{2}+xiy+iyx-y^{2}=(x^{2}-y^{2})+i(2xy)=u(x,y)+iv(x,y).$

Derivaatan olemassaolo voidaan todeta muodostamalla funktion reaali- ja imaginaariosien osittaisderivaatat

$u_{x}(x,y)={\partial u(x,y) \over \partial x}={\partial (x^{2}-y^{2}) \over \partial x}=2x-0=2x,$

$v_{y}(x,y)={\partial v(x,y) \over \partial y}={\partial (2xy) \over \partial y}=2x\cdot 1=2x,$

$u_{y}(x,y)={\partial u(x,y) \over \partial y}={\partial (x^{2}-y^{2}) \over \partial y}=0-2y=-2y$ ja

$v_{x}(x,y)={\partial v(x,y) \over \partial x}={\partial (2xy) \over \partial x}=2\cdot 1\cdot y=2y.$

Koska saadut osittaisderivaatat ovat polynomeina jatkuvia ja ne toteuttavat Cauchyn–Riemannin yhtälöt

$u_{x}(x,y)=v_{y}(x,y)$

ja

$u_{y}(x,y)=-v_{x}(x,y),$

on funktio $f(z)=z^{2}$ derivoituva.

Kompleksifunktioiden derivointikaavat

Kompleksisten alkeisfunktioiden derivointisäännöt ja yleiset derivointisäännöt säilyvät samanlaisina kuin reaalimuuttujaisilla alkeisfunktioilla.

Usean muuttujan funktiot

Yhden muuttujan funktion derivointi voidaan yleistää vektoriarvoisen muuttujan vektoriarvoiseen funktion derivaattaan. Vektorilla voidaan esittää useamman muuttujan funktion määrittelyjoukkoa. Funktion kuvaus on tällöin $f:\mathbb {R} ^{n}\to \mathbb {R}$. Vektoreissa voidaan käyttää myös kompleksimuuttujia. Derivaatta määritellään tällaisilla funktioilla luonnollisella tavalla.

Osittaisderivaatta

Reaaliarvoisille usean muuttujan funktiolle voidaan määritellä osittaisderivaatta, joka on tavallinen derivaatta yhden muuttujansa suhteen. Osittaisderivoitaessa yhtä muuttujaa, muita muuttujia kohdellaan kuin vakioita. Sitä käytetään, kun halutaan tietää yhden muuttujan muutoksen vaikutus funktion arvoihin.

Suunnattu derivaatta

Reaaliarvoisille usean muuttujan funktiolle voidaan määritellä suunnattu derivaatta, joka on tavallinen derivaatta yhdessä pisteessä halutussa suunnassa. Kussakin määrittelyjoukon pisteessä voidaan funktiolle määrittää suunnattu derivaatta äärettömän moneen eri suuntaan. Erisuuntaiset derivaatat ovat arvoltaan usein erisuuruisia. Ne voidaan laskea kätevästi käyttäen gradienttia. Sunnatulla derivaatalle voidaan määrittää myös toispuoleinen derivaatta.

Sovelluksia

Esimerkki derivoidusta paraabelista.

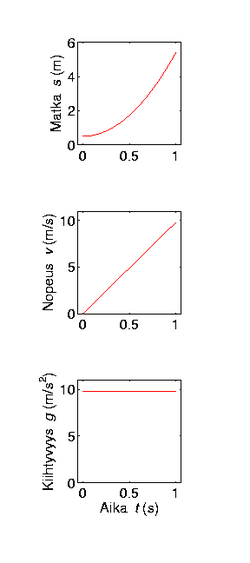
Derivointi on hyödyllinen matemaattinen apuneuvo myös teknisissä tieteissä. Seuraavassa yksinkertainen esimerkki derivaatan käytöstä fysiikassa. Oletetaan, että halutaan selvittää vaikkapa putoamiskiihtyvyys $g\,$, kun mitataan putoavan pallon putoama matka $s\,$ ajan $t\,$ funktiona. Tiedetään, että matka voidaan ilmaista

$s=s_{0}+{\frac {1}{2}}gt^{2},\,$

ja nopeus $v\,$ on matkan derivaatta ajan suhteen

$v={\frac {ds}{dt}}={\frac {d}{dt}}\left(s_{0}+{\frac {1}{2}}gt^{2}\right)={\frac {1}{2}}g\ 2t=gt,$

mistä edelleen kiihtyvyys $g\,$ on nopeuden derivaatta ajan suhteen. Toisin sanoen siis matkan toinen derivaatta:

${\frac {d^{2}s}{dt}}={\frac {dv}{dt}}={\frac {d}{dt}}\left(gt\right)=g.\$

Kun mitattu etäisyys derivoidaan ajan suhteen numeerisesti, saadaan kiihtyvyys. Ajan suhteen derivoitaessa saatetaan joskus myös käyttää derivaatan merkkinä pistettä derivoitavan suureen päällä ${\frac {dx}{dt}}={\dot {x}}$ ja ${\frac {d^{2}x}{dt}}={\ddot {x}}$.

Historia

Aluksi tutkittiin suureiden muuttumista kun muuttujien arvoa muutettiin. Suureen muutosnopeuden arvo riippui käytettävästä muuttujan arvon muutossuuruudesta ja se saatiin sitä paremmaksi, mitä pienempi oli muutujan muutosväli. Käyttöön otettiin infinitesimaalin käsite. Se vastasi "pienintä mahdollista muutosta" suureen arvossa. Derivaatta määritettiin siksi funktion arvon muutosnopeudeksi, kun muuttuja muuttui vain infinitesimaalisen vähän. Infinitesimaalit on 1900-luvulta asti korvattu raja-arvon käsitteellä, jossa muutosnopeuden keskiarvo on annetulla välillä korvattu erotusosamäärällä. Kun annettua väliä pienennetään rajatta, saadaan derivaatan arvo erotusosamäärän raja-arvona.

Derivaatan käsitteen esittivät ensimmäisenä Isaac Newton ja Gottfried Leibniz 1600-luvulla. Sanan derivaatta (johdos) otti käyttöön Joseph-Louis Lagrange 1700-luvun lopulla.

Katso myös

• Osittaisderivaatta
• Integraalifunktio
• Jatkuva funktio
• Gradientti

Lähteet

• Alatupa, Sami & Hassinen, Sanna & Hemmo, Katariina & Leikas, Mika: Pitkä Sigma 7. (lukion pitkän matematiikan oppikirja). Helsinki: Sanoma Pro, 2014. ISBN 978-952-63-0307-9.
• Hurri-Syrjänen, Ritva: Differentiaali- ja integraalilaskenta I, (luentomoniste), Helsingin yliopisto, 1999

Aiheesta muualla

• Matematiikan etäopiskeluympäristö, Derivaatta – Opetus.tv
• "Newton, Leibniz, and Usain Bolt" – Khan Academy (englanniksi)
• "Derivative" – MathWorld (englanniksi)