Kvasisäännöllinen monitahokas
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Kvasisäännöllinen monitahokas on semiregulaarinen monitahokas, jolla on sivutahkoina kahdenlaisia säännöllisiä monikulmioita, jotka vuorottelevat monitahokkaan jokaisen kärjen ympärillä. Ne ovat särmätransitiivisia, eli ne voidaan kuvata yhtenevyyskuvauksella itselleen siten, että mikä tahansa niiden särmistä voi kuvautua mille tahansa toiselle, ja tässä suhteessa ne muistuttavat säännöllisiä monitahokkaita enemmän kuin semiregulaariset monitahokkaat, jotka ovat vain kärkitransitiivisia.
Kvasisäännöllisten monitahokkaiden duaalikappaleita sanotaan myös joskus kvasisäännöllisiksi. Ne kuitenkaan eivät ole kärkitransitiivisia, mutta kylläkin tahkotransitiivisia, ja niissä vuorottelee kaksi erilaista säännöllistä kärkikuviota.
On olemassa vain kaksi kuperaa kvasisäännöllistä monitahokasta, kuboktaedri ja ikosidodekaedri[1]. Nämä Keplerin antamat nimet perustuvat siihen, että edellinen voidaan konstruoida kuutiosta ja sen duaalikappaleesta, oktaedrista, joilla on yhteinen keskipiste jälkimmäinen vastaavasti ikosaedrista ja sen duaalikappaleesta, dodekaedrista. Näissä konstruktioissa kvasisäännöllisen monitahokkaan muodostaa kahden sellaisen säännöllisen monitahokkaan leikkaus eli molempien sisään jäävä avaruuden alue, joilla on yhteinen keskipiste.[1]
Nämä muodot, jotka edustavat säännöllisen kuvion ja sen duaalin muodostamaa paria, voidaan esittää Schläflin symboleilla tai r{p,q}, jotka osoittavat, että niihin sisältyvät sekä säännöllisen monitahokkaan {p,q} että sen duaalikappaleen {q,p} sivut.[1] Tämän symbolin kuvaamalla kvasisäännöllisellä monitahokkaalla on kärkikonfiguraatio p.q.p.q (tai (p.q)2).
Yleisemmin uniformisella kvasisäännöllisellä kuviolla voi olla kärkikonfiguraatio (p.q)r, joka esittää r (2 tai useampaa) tapausta tahkoista kärjen ympärillä.
Myös tason tessellaatiot eli laatoitukset voivat olla kvasisäännöllisiä, erityisesti triheksagonaalinen laatoitus, jonka kärkikonfiguraatio on (3.6)2. Hyperbolisella tasolla on muitakin kvasisäännöllisiä laatoituksia kuten triheptagonaalinen laatoitus, (3.7)2, sekä yleisemmin (p.q)2, missä 1/p+1/q<1/2.
Sellaiset säännölliset monitahokkaat ja laatoitukset, joissa jokaisen kärjen ympärillä on parillinen määrä tahkoja, voidaan myös käsittää kvasisäännöllisiksi jakamalla sellaisetkin sivutahkot, joilla on sama määrä sivuja, kahteen ryhmään, joita käsitellään eri tavalla. Ne voivat esimerkiksi olla eri värisiä. Säännöllinen kuvio, jonka Schläflin symboli on {p,q}, voidaan käsittää kvasisäännölliseksi kärkikonfiguraatiolla (p.p)q/2, jos q on parillinen.
Täten oktaedri voidaan käsittää kvasisäännölliseksi tetratetraedriksi, jossa on osia kahden tetraedrin kolmiomaisista sivutahkoista, (3a.3b)2, värittämällä ne kahdella eri värillä. Samaan tapaan neliölaatoitusta (4a.4b)2, voidaan pitää kvasisäännöllisenä, jos sen ruudut on väritetty kahdella värillä shakkilaudan tavoin. Myös kolmiolaatoituksessa laatat voidaan vastaavalla tavalla värittää kahdella eri värillä, (3a.3b)3.
Wythoffin konstruktio[muokkaa | muokkaa wikitekstiä]
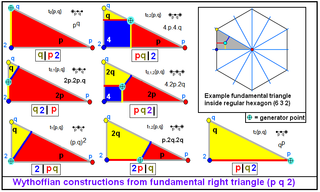 Säännölliset (p | 2 q) ja kvasisäännölliset monitahokkaat (2 | p q) voidaan konstruoida Wythoffin konstruktiolla käyttämällä lähtökohtana yhtä perusalueen kolmesta kärkipisteestä. Tämä määrittelee perusalueelle yhden erityisen särmän. |

q | 2 p, p | 2 q, 2 | p q
Coxeter määritteli kvasisäännöllisen monitahokkaan sellaiseksi, jonka Wythoffin symboli on muotoa p | q r, ja se on säännöllinen, jos q=2 tai q=r.[2]
Coxeterin–Dynkinin diagrammi on toinen symbolinen esitystapa, joka osoittaa kvasisäännöllisen relaation kahden duaalisen säännöllisen kappaleen välillä:
| Schläflin symboli | Coxeterin diagrammi | Wythoffin symboli | |
|---|---|---|---|
| {p,q} | q | 2 p | ||
| {q,p} | p | 2 q | ||
| r{p,q} | 2 | p q | ||
Kuperat kvasisäännölliset monitahokkaat[muokkaa | muokkaa wikitekstiä]
Varsinaisia kuperia kvasisäännöllisiä monitahokkaita on kaksi: kuboktaedri ja ikosidodekaedri. Molemmat kuuluvat myös Arkhimedeen kappaleisiin.[3] Lisäksi oktaedria, joka on samalla säännöllinen monitahokas, voidaan pitää myös kvasisäännöllisenä, jos sen sivut väritetään vuorotellen eri väreillä. Tässä muodossa siitä käytetään toisinaan nimitystä tetratetraedri.
Kuperien kvasisäännöllisten monitahokkaiden Schläflin symbolit, kärkikonfiguraatiot, Coxeterin diagrammit ja Wythoffin symbolit (oktaedri mukaan luettuna) ovat seuraavat:
| monitahokas | Schläflin symboli | Kärkikonfiguraatio | Coxeterin diagrammi | Wythoffin symboli | |
|---|---|---|---|---|---|
| Kuboktaedri | 2{3,4} | (3.4)2 | 2 | 3 4 | ||
| Ikosidodekaedri | 2{3,5} | (3.5)2 | 2 | 3 5 | ||
| Oktaedri | 2{3,3} | (3.3)2 | 2 | 3 3 | ||
Sekä kuboktaedri että ikosidodekaedri ovat samalla kahden keskenään duaalisen säännöllisen monitahokkaan yhteisiä ydinosia.[3] Niiden nimet viittaavat niihin monitahokaspareihin, joista ne voidaan täten muodostaa: sana kuboktaedri on muodostettu lisäämällä sanaan oktaedri etuliite kub-, joka johtuu kuutiota tarkoittavasta sanasta cube, ja vastaavasti sana ikosidodekaedri on yhdistetty sanoista ikosaedri ja dodekaedri. Vastaavalla tavalla oktaedri on kahden keskenään duaalisen tetraedrin yhteinen ydinosa[3] (nimellä stella octangula tunnettu muodostelma), ja tällä tavoin muodostettuna sitä sanotaan joskus myös tetratetraedriksi.
| Säännöllinen | Säännöllinen duaali | Kvasisäännöllinen | Särmäkuvio |
|---|---|---|---|
 Tetraedri {3,3} 3 | 2 3 |
 Tetraedri {3,3} 3 | 2 3 |
 Tetratetraedri r{3,3} 2 | 3 3 |
 3.3.3.3 |
 Kuutio {4,3} 3 | 2 4 |
 Oktaedri {3,4} 4 | 2 3 |
 Kuboktaedri r{3,4} 2 | 3 4 |
 3.4.3.4 |
 Dodekaedri {5,3} 3 | 2 5 |
 Ikosaedri {3,5} 5 | 2 3 |
 Ikosidodekaedri r{3,4} 2 | 3 5 |
 3.5.3.5 |
Kumpikin kvasisäännöllinen monitahokas voidaan konstruoida typistämällä jompikumpi sen muodostavista säännöllisestä monitahokkaasta leikkaamalla siitä jokaisesta kärjestä pois niin suuri pala, että alkuperäisen monitahokkaan jokainen sivu kutistuu yhdeksi pisteeksi.
Kvasisäännölliset laatoitukset[muokkaa | muokkaa wikitekstiä]
Tätä sarjaa edustaa triheksagonaalinen laatoitus, jonka kärkikuvio on (3.6)2. Se on 'kvasisäännöllinen laatoitus, joka on yhdistelmä kolmio- ja kuusikulmiolaatoituksesta samaan tapaan kuin kvasisäännölliset monitahokkaat ovat kahden säännöllisen monitahokkaan yhdistelmiä.
| Säännöllinen | Säännöllinen duaali | Kvasisäännöllinen | Kärkikuvio |
|---|---|---|---|
 Heksagonaalinen laatoitus {6,3} 6 | 2 3 |
 Kolmiolaatoitus {3,6} 3 | 2 6 |
 Triheksagonaalinen laatoitus r{6,3} |
 (3.6)2 |
Shakkilautamalli on neliölaatoituksen kvasisäännöllinen väritys, jonka kärkikuvio on (4.4)2:
| Säännöllinen | Säännöllinen duaali | Kvasisäännöllinen | Kärkikuvio |
|---|---|---|---|
 {4,4} 4 | 2 4 |
 {4,4}
|
 r{4,4} 2 | 4 4 |
 (4.4)2 |
Kolmiolaatoitus voidaan myös käsittää kvasisäännölliseksi. Sen muodostavat kolme vuorottelevaa kolmioiden joukkoa jokaisen kärjen ympärillä, (3.3)3:
 h{6,3} 3 | 3 3 |
Hyperbolisella tasolla sarja jatkuu edelleen. Siihen kuuluu muun muassa triheptagonaalinen laatoitus jonka kärkikuvio on (3.7)2. Se on kvasisäännöllinen laatoitus, jonka saadaan yhdistelmänä kertaluvun 7 kolmiolaatoituksesta ja heptagonaalisesta eli seitsenkulmioiden muodostamasta laatoituksesta:
| Säännöllinen | Säännöllinen duaali | Kvasisäännöllinen | Kärkikuvio |
|---|---|---|---|
 Heptagonaalinen laatoitus {7,3} 7 | 2 3 |
 Kolmiolaatoitus {3,7} 3 | 2 7 |
 Triheptagonaalinen laatoitus r{3,7} 2 | 3 7 |
 (3.7)2 |
Ei-kuperia esimerkkejä[muokkaa | muokkaa wikitekstiä]
Vuonna 1954 H.S.M. Coxeter luokitteli myös muutamat samantapaiset tähtimonitahokkaat kvasisäännöllisiksi.[4]
Kaksi niistä voidaan muodostaa säännöllisten Kepler-Poinsotin kappaleiden duaalipareista samaan tapaan kuin edellä mainitut kuperat kvasisäännölliset kappaleet, nimittäin suuri ikosidodekaedri ja dodekadodekaedri [3]:
Näiden lisäksi on vielä yhdeksän hemipolyedriä, jotka saadaan leikkaamalla edellä mainituista kvasisäännöllisistä monitahokkaista paloja pois. Niissä on mukana ekvatoriaalisia tahkoja, jotka kulkevat alkuperäinen monitahokkaan keskipisteen kautta:
| Kvasisäännöllinen (typistetty) |  Tetratetraedri |
 Kuboktaedri |
 Ikosidodekaedri |
 Suuri ikosidodekaedri |
 Dodekadodekaedri |
|---|---|---|---|---|---|
| Kvasisäännöllinen (hemipolyedri) |  Tetrahemihekeaedri 3/2 3 | 2 |
 Oktahemioktaedri 3/2 3 | 3 |
 Pieni ikosihemidodekaedri 3/2 3 | 5 |
 Suuri ikosihemidodekaedri 3/2 3 | 5/3 |
 Pieni dodekahemikosaedri 5/3 5/2 | 3 |
| Kärkikuvio |  3.4.3/2.4 |
 3.6.3/2.6 |
 3.10.3/2.10 |
 3.10/3.3/2.10/3 |
 5/2.6.5/3.6 |
| Kvasisäännöllinen (hemipolyedrit) |  Kubohemioktaedri 4/3 4 | 3 |
 Pieni dodekahemidodekaedri 5/4 5 | 5 |
 Suuri dodekahemidodekaedri 5/3 5/2 | 5/3 |
 Suuri dodekahemidodekaedri 5/4 5 | 3 | |
| Kärkikuvio |  4.6.4/3.6 |
 5.10.5/4.10 |
 5/2.10/3.5/3.10/3 |
 5.6.5/4.6 |
Sitä paitsi on kolme ditrigonaalista muotoa, jotka kaikki saadaan poistamalla palasia säännöllisestä dodekaedrista. Niiden kärkikuvioina esiintyy kolme muunelmaa kahdesta tahkotyypistä:
| Kuva | Monitahokkaan nimi Wythoffin symboli Coxeterin diagrammi |
Kärkikuvio |
|---|---|---|

|
Ditrigonaalinen dodekadodekaedri 3 | 5/3 5 |
 (5.5/3)3 |

|
Pieni trigonaalinen ikosaedri 3 | 5/2 3 |
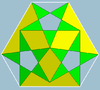 (3.5/2)3 |

|
Suuri ditrigonaalinen ikosidodekaedri 3/2 | 3 5 |
 ((3.5)3)/2 |
Euklidisella tasolla hemipolyedrien sarjaa jatkavat seuraavat neljä tähtimäistä laatoitusta eli tessellaatiota, joissa apeirogonit vastaavat edellä mainittuja ekvatoriaalisia monitahokkaita:
Kvasisäännölliset duaalit[muokkaa | muokkaa wikitekstiä]
Jotkut kirjoittajat ovat sitä mieltä, että kun kvasisäännöllisten kappaleiden duaalikappaleilla on sama symmetria, näitä duaalikappaleitakin pitäisi nimittää kvasisäännöllisiksi. Kaikki eivät tätä terminologiaa kuitenkaan käytä. Nämä duaalikappaleet ovat transitiivisia särmiensä ja tahkojensa, mutta eivät kärkiensä suhteen; ne ovat särmätransitiivisia Catalanin kappaleita. Niistä kuperia ovat seuraavat:
- rombidodekaedri, jolla on kahdenlaisia kärkiä: kahdeksan kärkeä, joissa kolme neljäkkään muotoista tahkoa kohtaa toisensa, sekä kuusi kärkeä, joissa neljä tällaista tahkoa kohtaa toisensa.
- rombinen triakontaedri, jolla on kahdenlaisia kärkiä: 20 kärkeä, joissa kolme neljäkkään muotoista tahkoa kohtaa toisensa, sekä 12 kärkeä joissa viisi tällaista tahkoa kohtaa toisensa.
Sitä paitsi oktaedrin duaalikappale, kuutio, jota yleensä pidetään säännöllisenä monitahokkaata, voidaan käsittää myös kvasisäännölliseksi värittämällä sen kärjet vuorotellen eri väreillä.
Näiden tahkokonfiguraatiot ovat muotoa V3.n.3.n, ja Coxeterin–Dynkinin diagrammi on ![]()
![]()
![]()
![]()
![]() .
.

|
|

|

|

|

|
| Kuutio V(3.3)2 |
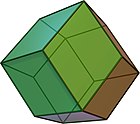
Rombidodekaedri V(3.4)2 |
Rombinen triakontaedri V(3.5)2 |
Rombinen laatoitus V(3.6)2 |
V(3.7)2 |
V(3.8)2 |
Näillä kvasisäännöllisillä duaaleilla on sivutahkoina vinoneliöitä eli neljäkkäitä. Niiden sarjaa jatkaa rombinen laatoitus, V(3.6)2.
Kvasisäännölliset polytoopit ja hunajakennot[muokkaa | muokkaa wikitekstiä]
Korkeammissa ulottuvuuksissa Coxeter määritteli kvasisäännöllisen polytoopin tai hunajakennon sellaiseksi, jolla on säännölliset sivut ja kvasisäännölliset kärkikuviot. Tästä seuraa, että sen kaikki kärkikuviot ovat yhtenevät ja että siinä vuorottelevat kahdenlaiset sivut.[5]
Euklidisessa 4-avaruudessa säännööllinen 16-solu voidaan myös käsittää kvasisäännölliseksi, vuodottelevaksi tesseraktiksi, h{4,3,3}, jonka Coxeterin diagrammi on: ![]()
![]()
![]()
![]()
![]()
![]()
![]() =
= ![]()
![]()
![]()
![]()
![]() ja joka muodostuu vuorottelevista tetraedrisistä soluista. Sen kärkikuvio on kvasisäännöllinen tetratetraedri eli oktaedri, jolla on tetraedrinen symmetria,
ja joka muodostuu vuorottelevista tetraedrisistä soluista. Sen kärkikuvio on kvasisäännöllinen tetratetraedri eli oktaedri, jolla on tetraedrinen symmetria, ![]()
![]()
![]()
![]()
![]()
Euklidisessa 3-avaruudessa ainoa kvasisäännöllinen hunajakenno on vuorotteleva kuutiollinen hunajakenno h{4,3,4}, jonka Coxeterin diagrammi on seuraavanlainen: ![]()
![]()
![]()
![]()
![]()
![]()
![]() . Se muodostuu vuorottelevista tetraedrin ja oktaedrin muotoisista soluista. Sen kärkikuvio on kvasisäännöllinen kuboktaedri,
. Se muodostuu vuorottelevista tetraedrin ja oktaedrin muotoisista soluista. Sen kärkikuvio on kvasisäännöllinen kuboktaedri, ![]()
![]()
![]()
![]()
![]() .[5]
.[5]
Hyperbolisessa 3-avaruudessa muuan kvasisäännöllinen hunajakenno on vuorotteleva kertaluvun 5 kuutiollinen hunajakenno, h{4,3,5}, jonka Coxeterin diagrammit ovat: ![]()
![]()
![]()
![]()
![]()
![]()
![]() =
= ![]()
![]()
![]()
![]()
![]() . Se koostuu vuorottelevista tetraedrisista ja ikosaedrisistä soluista. Sen kärkikuvio on kvasisäännöllinen ikosidodekaedri,
. Se koostuu vuorottelevista tetraedrisista ja ikosaedrisistä soluista. Sen kärkikuvio on kvasisäännöllinen ikosidodekaedri, ![]()
![]()
![]()
![]()
![]() . Se on sukua parakompaktille vuorottelevalle kertaluvun 6 kuutiolliselle hunajakennolle, h{4,3,6}, jossa vuorottelevat tetraedriset ja kuusikulmaiset solut ja jonka kärkikuvio on kvasisäännöllinen triheksagonaalinen laatoitus,
. Se on sukua parakompaktille vuorottelevalle kertaluvun 6 kuutiolliselle hunajakennolle, h{4,3,6}, jossa vuorottelevat tetraedriset ja kuusikulmaiset solut ja jonka kärkikuvio on kvasisäännöllinen triheksagonaalinen laatoitus, ![]()
![]()
![]()
![]()
![]() .
.
| Kvasisäännölliset polykoorit ja hunajakennot: h{4,p,q} | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Avaruus | Äärellinen | Affiininen | Kompakti | Parakompakti | |||||||
| Schäflin symboli |
h{4,3,3} | h{4,3,4} | h{4,3,5} | h{4,3,6} | h{4,4,3} | h{4,4,4} | |||||
| Coxeterin diagrammi |
|||||||||||
| Kuva | 
|

|

|

| |||||||
| Kärkikuvio r{p,3} |
 |
 |
 |
 |
 |
 | |||||
Muotoa {p,3,4) tai ![]()
![]()
![]()
![]()
![]()
![]()
![]() olevien polytooppien ja hunajakennojen symmetria voidaan puolittaa:
olevien polytooppien ja hunajakennojen symmetria voidaan puolittaa: ![]()
![]()
![]()
![]()
![]()
![]()
![]() , jolloin saadaan kvasisäännöllinen muoto
, jolloin saadaan kvasisäännöllinen muoto ![]()
![]()
![]()
![]()
![]() , jolla eri väriset {p, 3}-solut vuorottelevat. Tällaisiin tapauksiin kuuluu euklidinen kuutiollinen hunajakenno {4,3,4} kuutiomaisine soluineen, kompakti hyperbolinen {4,3,4} kenno dodekaedrin muotoisine soluineen sekä parakompakti {6,3,4}, äärettöminen kuusikulmaisen laatoituksen mukaisine soluineen. Niissä on neljä solua jokaisen kärjen ympärillä vuorottelevin värein. Niiden kärkikuviot ovat kvasisäännöllisiä tetratetraedrejä,
, jolla eri väriset {p, 3}-solut vuorottelevat. Tällaisiin tapauksiin kuuluu euklidinen kuutiollinen hunajakenno {4,3,4} kuutiomaisine soluineen, kompakti hyperbolinen {4,3,4} kenno dodekaedrin muotoisine soluineen sekä parakompakti {6,3,4}, äärettöminen kuusikulmaisen laatoituksen mukaisine soluineen. Niissä on neljä solua jokaisen kärjen ympärillä vuorottelevin värein. Niiden kärkikuviot ovat kvasisäännöllisiä tetratetraedrejä, ![]()
![]()
![]()
![]()
![]() =
= ![]()
![]()
![]() .
.



 , joka on sama kuin säännöllinen oktaedri.
, joka on sama kuin säännöllinen oktaedri.Samaan tapaan muotoa {p,3,6} tai ![]()
![]()
![]()
![]()
![]()
![]()
![]() olevien säännöllisten hyperbolisten hunajakennojen symmetria voidaan puolittaa:
olevien säännöllisten hyperbolisten hunajakennojen symmetria voidaan puolittaa: ![]()
![]()
![]()
![]()
![]()
![]()
![]() , jolloin saadaan kvasisäännölliset muodot
, jolloin saadaan kvasisäännölliset muodot ![]()
![]()
![]()
![]()
![]() , joilla eri väriset {p,3} -solut vuorottelevat. Niissä jokaisen särmän ympärillä on kuusi solua, joilla vuorottelee kaksi väriä. Niiden kärkikuviot ovat kvasisäännöllisiä kolmiolaatoituksia,
, joilla eri väriset {p,3} -solut vuorottelevat. Niissä jokaisen särmän ympärillä on kuusi solua, joilla vuorottelee kaksi väriä. Niiden kärkikuviot ovat kvasisäännöllisiä kolmiolaatoituksia, ![]()
![]()
![]() .
.





 =
= 


| Muoto | Parakompaktit | Ei-kompaktit | |||||
|---|---|---|---|---|---|---|---|
| Nimi | Kertaluvun 6 tetraedrinen {3,3,6} {3,3[3]} |
Kertaluvun 6 kuutiollinen {4,3,6} {4,3[3]} |
Kertaluvun 6 dodekaedrinen {5,3[3]} |
Kertaluvun 6 heksagonaalinen {6,3,6} {6,3[3]} |
Kertaluvun 3-6 heptagonaalinen {7,3,6} {7,3[3]} |
Kertaluvun 3-6 oktagonaalinen {8,3,6} {8,3[3]} |
Kertaluvun 3-6 apeirogonaalinen {∞,3,6} {∞,3[3]} |
| Kuva | 
|

|

|

|

|

|

|
| Solut | {3,3} |
{4,3} |
{5,3} |
{6,3} |
{7,3} |
{8,3} |
|
Lähteet[muokkaa | muokkaa wikitekstiä]
- P. Cromwell: Polyhedra. Cambridge University Press, 1977.
- H.S.M. Coxeter: Regular Polytopes (3rd ed.), s. 17, 69. Dover Edition, 1973. ISBN 0-486-61480-8.
Viitteet[muokkaa | muokkaa wikitekstiä]
- ↑ a b c Quasiregular Polyhedron Wolfram MathWorld. Eric Weisstein. Viitattu 2.11.2018.
- ↑ H. S. M. Coxeter, M. S. Longuet-Higgins, J. C. P. Miller: Uniform Polyhedra. (Kappale 7, The regular and quasiregular polyhedra p) Philosophical Transactions of the Royal Society of London, 1954, nro 246 A, s. 401–450.
- ↑ a b c d Quasiregular Polyhedra George W. Hart. Viitattu 2.11.2018.
- ↑ Uniform Polyhedron Wolfram MathWorld. Eric W. Weisstein. Viitattu 2.11.2018.
- ↑ a b H. S. M. Coxeter: ”Other honeycombs”, Regular Polytopes, s. 69, 88. {{{Julkaisija}}}.
































































