Konstruoituva monikulmio

Konstruoituva monikulmio on säännöllinen monikulmio, joka voidaan piirtää geometrisella konstruktiolla eli ainoastaan harppia ja viivoitinta käyttäen. Esimerkiksi säännöllinen viisikulmio voidaan konstruoida harpilla ja viivoittimella, kun taas säännöllistä seitsenkulmiota ei voida. Konstruoituvia monikulmioita on olemassa äärettömän monta, mutta niistä sellaisia, joissa sivujen lukumäärä on pariton, tunnetaan vain 31 erilaista.
Konstruoituvuuden edellytykset[muokkaa | muokkaa wikitekstiä]

Säännöllinen kolmi- ja nelikulmio eli tasasivuinen kolmio ja neliö sekä säännöllinen kuusikulmio on helppo konstruoida harpilla ja viivoittimella. Säännöllisen viisikulmion konstruointi on jo hankalampaa, mutta jo antiikin Kreikan matemaatikot tunsivat menetelmän, jolla se voidaan tehdä.[1] Lisäksi he osasivat konstruoida säännöllisen monikulmion, jonka sivujen lukumäärä on kaksi kertaa niin suuri kuin annetussa säännöllisessa monikulmiossa.[2] Tämä herätti kysymyksen: voidaanko kaikki säännölliset monikulmiot konstruoida harpilla ja viivoittimella? Jos ei, mitkä n-kulmiot (missä n on sivujen lukumäärä) voidaan täten konstruoida, mitkä ei?
Carl Friedrich Gauss todisti vuonna 1796, että säännöllinen 17-kulmio on konstruoituva. Viisi vuotta myöhemmin hän kehitti Gaussin jaksojen teorian teoksessaan Disquisitiones Arithmeticae. Tämä teoria teki hänelle mahdolliseksi muotoilla riittävän ehdon säännöllisen monikulmion konstruoituvuudelle. Hän väitti, että sama ehto oli myös välttämätön, mutta hän ei koskaan julkaissut todistusta tälle väitteelle. Täydellisen todistuksen esitti Pierre Wantzel vuonna 1837. Tulos tunnetaan Gaussin-Wantelin lauseena:
- Säännöllinen n-kulmio voidaan konstruoida harpilla ja viivoittemella, jos ja vain jos n joko on jokin 2:n potenssi tai se voidaan esittään 2:n potenssin sekä yhden tai useamman toisistaan poikkeavan Fermat’n alkuluvun tulona.
Fermat’n alkuluvut ovat alkulukuja, jotka voidaan esittää muodossa (Itse asiassa kaikki alkuluvut, jotka voidaan esittää muodossa , missä n on kokonaisluku, ovat samalla Fermat’n alkulukuja, sillä jos n ei ole kahden potenssi, se voidaan esittää tulona , missä on kahden potenssi ja p jokin pariton luku. Jos luvulle käytetään merkintää q, saadaan , ja kun 1 on pariton, on aina jaollinen :lla, olipa q mikä positiivinen kokonaisluku tahansa.)
Geometrinen probleema voidaan palauttaa puhtaasti lukuteoreettiseen probleemaan käyttämällä hyväksi sitä seikkaa, että n-kulmio on konstruoituva, jos ja vain jos kulman on konstruoituva luku, toisin sanoen sille voidaan esittää tarkka arvo neljän aritmeettisen peruslaskutoimituksen sekä neliöjuurien oton avulla.[3] Yhtäpitävästi n-kulmio on konstruoituva, jos n:nnen syklotomisen polynomin nollakohdat ovat konstruoituvia.
Gaussin–Wantzelin lause ja sen seurauksia[muokkaa | muokkaa wikitekstiä]
Gaussin–Wantzelin lause voidaan ilmaista seuraavasti:
- Säännöllinen n-kulmio voidaan konstruoida harpilla ja viivoittimella, jos ja vain jos n = 2kp1p2...pt, missä k ja t ovat ei-negatiivisia kokonaislukuja ja luvut pi (missä t > 0) toisitaan poikkeavia Fermat’n alkulukuja.
Tunnettuja Fermat’n alkulukuja ovat vain seuraavat viisi:
Koska Fermat’n alkuluvuista voidaan muodostaa 31 kombinaatiota, joissa niitä on yhdestä viiteen, on 31 tunnettua konstruoituvaa monikulmiota, joiden sivujen lukumäärä on pariton.
Seuraavista 26 Fermat’n luvusta, F5:stä F30:een, yksikään ei ole alkuluku. F31:sta ja sitä suuremmista Fermat’n luvuista asiaa ei tiedetä.[3]
Säännöllinen n-kulmio on siis konstruoituva, jos luku n on esimerkiksi jokin seuraavista:
- n = 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 32, 34, 40, 48, 51, 60, 64, 68, 80, 85, 96, 102, 120, 128, 136, 160, 170, 192, 204, 240, 255, 256, 257, 272, 320, 340, 384, 408, 480, 510, 512, 514, 544, 640, 680, 768, 771, 816, 960, 1020, 1024, 1028, 1088, 1280, 1285, 1360, 1536, 1542, 1632, 1920, 2040, 2048, ... (A003401 OEIS-tietokannassa,
kun taas se ei ole konstuoitavissa harpilla ja viivoittimella, jos n on jokin seuraavista:
- n = 7, 9, 11, 13, 14, 18, 19, 21, 22, 23, 25, 26, 27, 28, 29, 31, 33, 35, 36, 37, 38, 39, 41, 42, 42, 43, 44, 45, 46, 47, 49, 50, 52, 53, 54, 55, 56, 57, 58, 59, 61, 62, 63, 65, 66, 67, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 81, 82, 83, 84, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 97, 98, 99, 100, 101, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 121, 122, 123, 124, 125, 126, 127, ... (A004169 OEIS-tietokannassa).
Kytkentä Pascalin kolmioon[muokkaa | muokkaa wikitekstiä]
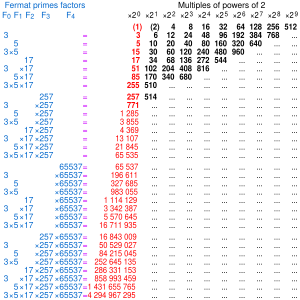
Koska tunnettuja Fermat’n alkulukuja on viisi, tunnetaan 31 lukua, jotka ovat yhden tai useamman toisistaan poikkeavan Fermat’n alkuluvun tuloja ja näin ollen 31 konstruitavaa monikulmiota, joissa sivujen lukumäärä on pariton. Nämä luvut ovat 3, 5, 15, 17, 51, 85, 255, 257, 771, 1285, 3855, 4369, 13107, 21845, 65535, 65537, 196611, 327685, 983055, 1114129, 3342387, 5570645, 16711935, 16843009, 50529027, 84215045, 252645135, 286331153, 858993459, 1431655765, 4294967295 A045544 OEIS-tietokannassa. John Conway totesi kirjassaan The Book of Numbers, että jos nämä luvut kirjoitetaan binäärilukuina, ovat samat, jotka muodostavat modulaariaritmeettisen Pascalin kolmion modulo 2 ensimmäiset 32 riviä, lukuun ottamatta ensimmäistä, jossa on vain luku 1 ja joka vastaa "yksikulmiota". Niinpä tällaisessa kolmiossa ykköset muodostavat approksimaation Sierpinskin kolmiolle. Tämä malli ei kuitenkaan päde enää pidemmälle, sillä seuraava Fermat’n luku on yhdistetty luku (4294967297 = 641 · 6700417), ja niinpä seuraavat rivit eivät vastaa konstruoituvia monikulmioita. Ei tiedetä, onko suurempia Fermat’n alkulukuja edes olemassa, ja näin ollen ei myöskään tiedetä, kuinka monta sellaista konstruoituvaa monikulmiota on olemassa, joissa sivujen lukumäärä on pariton. Jos Fermat’n alkulukuja on olemassa q kappaletta, on olemassa 2q-1 sellaista monikulmiota.
Modulaariaritmeettinen Pascalin kolmio modulo 2 sisältää vain lukuja 0 ja 1, ja se saadaan tavanomaisesta Pascalin kolmiosta vaihtamalla siinä kaikki parittomat luvut lukuun 1 ja kaikki parilliset luvut lukuun 0. Seuraavassa on kolmion kymmenen ensimmäistä riviä sekä niiden oikealla puolella eri rivit binääriluvuiksi tulkittuina ja muunnettuina kymmenjärjestelmään:
1 1
1 1 3
1 0 1 5
1 1 1 1 15
1 0 0 0 1 17
1 1 0 0 1 1 51
1 0 1 0 1 0 1 85
1 1 1 1 1 1 1 1 255
1 0 0 0 0 0 0 0 1 257
1 1 0 0 0 0 0 0 1 1 771
Yleinen teoria[muokkaa | muokkaa wikitekstiä]
Myöhempien Galois’n teoria koskevien tutkimusten valossa näiden todistusten perusteet ovat käyneet entistä selvemmiksi. Analyyttisen geometrian avulla on helppo todistaa, että konstruoituvien janojen pituuksien on oltava sellaisia, että ne saadaan perusjanojen pituuksista kertomalla ne sellaisilla luvuilla, jotka saadaan ratkaisemalla jokin sarja toisen asteen yhtälöitä.[4] Tällaiset pituudet muodostavat kuntalaajennukseen, joka saadaan suorittamalla useita neliöllisiä laajennuksia. Tästä seuraa, että konstuktioiden muodostaman kunnan aste peruskunnan suhteen on aina kahden potenssi.
Säännöllisten n-kulmioiden muodostamassa erityistapauksessa kysymys palautuu kysymykseen pituuksien
konstruoituvuudesta. Nämä ovat trigonometrisia lukuja ja niin ollen algebrallisia lukuja. Kukin tällainen luku kuuluu n:nteen syklotomiseen kuntaan — ja itse asiassa sen reaaliseen alikuntaan, joka on totaalisesti reaalinen kunta ja samalla rationaalikertoiminen vektoriavaruus, jonka Hamelin ulottuvuus on
- ½f(n),
missä f(n) on Eulerin φ-funktio. Wantzelin tulos seuraa laskuista, jotka osoittavat, että f(n) on kahden potenssi vain siinä tarkoitetuissa tapauksissa.
Gaussin konstruktiolle, kun Galois’n ryhmä on 2-ryhmä, tästä seuraa, että sillä on jono aliryhmiä, joiden alkioiden lukumäärät ovat
- 1, 2, 4, 8, ...
ja joista jokainen on seuraavan aliryhmä, mikä on helppo todistaa induktiolla, kun ryhmät ovat Abelin ryhmiä. Sen vuoksi syklotomisella kunnalla on sarja alikuntia, joista kunkin aste on 2 potenssiin edellisen sarjan aste. Sellaisten kuntien generaattorit voidaan muodostaa Gaussin jaksojen teorian avulla. Esimerkiksi 17-kulmiolla on tällaiset jaksot, joista yksi saadaan kahdeksan yksikköjuuren summa, toinen vastaavasti neljän ja kolmas kahden yksikköjuuren summana, joka ovat
Jokainen näistä juurista on jonkin sellaisen toisen asteen yhtälön ratkaisu, joka voidaan muodostaa edellisestä. Lisäksi näiden yhtälöiden ratkaisut ovat reaalilukuja, eivät kompleksisia, joten periaatteessa ne voidaan ratkaista geometrisella konstuktiolla, sillä tämä kaikki voidaan suorittaa pelkästään täysin reaalisen kunnan sisällä.
Täten Gaussin tulos voidaan ymmärtää nykyisin käsittein; suorittamalla ratkaistavilla yhtälöillä laskutoimituksia jaksot voidaan neliöidä ja verrata niitä alempiin jaksoihin täysin algoritmisin menetelmin.
Konstruktiot harpilla ja viivoittimella[muokkaa | muokkaa wikitekstiä]
Kaikista tunnetuista konstruoituvista monikulmioista tiedetään myös, miten ne voidaan konstruoida harpilla ja viivoittimella. Jos n = p·q, missä p = 2 taikka p ovat q keskenään jaottomia, n-kulmio voidaan konstruoida p- ja q-kulmioiden avulla.
- Jos p = 2, piirretään q-kulmio ja puolitetaan yksi sen keskuskulmista. Täten saadaan konstruoiduksi 2q-kolmio
- Jos p > 2, piirretään p-kulmio ja q-kulmio saman ympyrän sisään siten, että niillä on yksi yhteinen kärkipiste. Koska p ja q ovat keskenään jaottomia, on olemassa kokonaisluvut a ja b siten, että ap + bq = 1. Niinpä 2ap/q + 2bp/p = 2p/pq. Täten voidaan konstruoida p·q-kulmio.
Täten riittää selvittää, miten voidaan konstruoida sellaiset n-kulmiot, joissa n on Fermat’n alkuluku.
- Tasasivuisen kolmion konstruointi on helppoa ja tunnettiin jo antiikin aikana.[5]
- Jo Eukleides (teoksessaan Alkeet, noin 300 eKr.) ja Ptolemaios (teoksessaan Almagest) esittivät kumpikin myös menetelmänsä esitti teoksessaan Alkeet (noin 300 eKr.), myös, miten säännöllinen viisikulmio voidaan konstruoida.[1][6]
- Vaikka Gauss todistikin, että 17-kulmion konstruointi harpilla ja viivoittimella on mahdollista, hän ei esittänyt keinoa, miten se voidaan suorittaa. Ensimmäisen konstruktion keksi Erchinger muutamia vuosia myöhemmin.
- Ensimmäisen eksplisiittisen konstruktiomenetelmän säännölliselle 257-kulmiolle esitti Magnus Georg Paucker vuonna 1822.[7] Fiedrich Julius Richelot esitti oman menetelmänsä vuonna 1832.[8]
- Konstruktion säännölliselle 65537-kulmiolle esitti ensimmäisenä Johann Gustav Hermes. Konstruktio on hyvin monimutkainen, ja Hermes käytti kymmenen vuotta saadakseen valmiiksi asiaa käsittelevän 200-sivuisen käsikirjoituksen.[9]
Kuvia[muokkaa | muokkaa wikitekstiä]




Vasemmalta oikealle: säännöllisen 15-, 17-, 257- ja 65537-kulmion konstruktiot. Vain ensimmäinen vaihe 65537-kulmion konstruktiosta on merkitty, muiden konstruktiot on esitetty kokonaisuufessaan.
Muita konstruktioita[muokkaa | muokkaa wikitekstiä]
Edellä on käsitelty klassisia geometrisia konstruktioita, jotka voidaan suorittaa ainoastaan harppia ja viivoitinta käyttämällä. Muutkin kostruktiot tulevat mahdollisiksi, jos sallitaan myös muita työvälineitä. Esimerkiksi niin sanotuissa neusis-konstruktioissa käytetään myös merkittyä viivainta. Konstruktiot ovat matemaattisia idealisaatioita ja oletetaan, että ne voidaan suorittaa tarkasti.
Jos harpin ja viivoittimen lisäksi on käytettävissä väline, jolla kulma voidaan jakaa kolmeen yhtä suureen osaan, säännöllinen n-kulmio voidaan konstruoida, jos ja vain jos , missä r, s, k >= 0 ja missä luvut pi ovat toisistaan eroavia Pierpontin alkulukuja (eli muotoa olevia alkulukuja) ja suurempia kuin 3. Näin voidaan konstruktiot säännölliset 3n-kulmiot kuten 9-, 27- ja 81 ja niin edelleen sekä myös esimerkiksi 7- ja 13-kulmiot.[10] Tällä
Lähteet[muokkaa | muokkaa wikitekstiä]
- ↑ a b Eukleides: ”Book IV, Proposition 11”, Elementa. David E. Joyce, 1997. Teoksen verkkoversio.
- ↑ Benjamin Bold: Famous Problems of Geometry and How to Wolve Them, s. 49–50. Dover Publications, 1982.
- ↑ a b c Matti Lehtinen, Jorma Merikoski, Timo Tossavainen: ”Geometrisia konstruktioita”, Johdatus tasogeometriaan, s. 83. WSOY, 2007. ISBN 978-951-0-31232-2.
- ↑ David A. Cox: ”Theorem 10.1.6”, Galois Theory, s. 259. John Wiley & Sons, 2012. ISBN 978-1-118-07205-9. doi:10.1002/9781118218457.
- ↑ Eukleides: ”Book I, Proposition 1”, Elementa. David E. Joyce, 1997. Teoksen verkkoversio. (englanniksi)
- ↑ Klaudios Ptolemaios: ”Calculation of chord table (H32–H33)”, Almagest, s. 48. (englanniksi kääntänyt G. J. Toomer). Duckworth, 1984. ISBN 0-7156-1588-2. Teoksen verkkoversio.
- ↑ Magnus Georg Paucker: Geometrische Verzeichnung des regelmäßigen Siebzehn-Ecks und Zweyhundersiebenundfünfzig-Ecks in den Kreis. Jahresverhandlungen der Kurländischen Gesellschaft für Literatur und Kunst, 1822, nro 2, s. 160–219. Artikkelin verkkoversio. (saksaksi)
- ↑ Friedrich Julius Richelot: De resolutione algebraica aequationis x257 = 1, sive de divisione circuli per bisectionem anguli septies repetitam in partes 257 inter se aequales commentatio coronata. Journal für die reine und angewandte Mathematik, 1832, nro 9, s. 1–26, 146–161, 209–230, 337–358. doi:10.1515/crll.1832.9.337. Artikkelin verkkoversio. (latinaksi)
- ↑ Johann Gustav Hermes: Über die Teilung des Kreises in 65537 gleiche Teile. Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse, 1894, nro 3, s. 170–186. Göttingen: Artikkelin verkkoversio. (saksaksi)
- ↑ Andrew Mattei Gleason: Angle trisection, the heptagon, and the triskaidecagon. The American Mathematical Monthly, Maaliskuu 1988, 95. vsk, nro 3, s. 185–194. doi:10.2307/2323624. Artikkelin verkkoversio. Viitattu 30.8.2018.











