Isoterminen ilmakehä

Ilmakehätilavuuselementtiin vaikuttavat voimat. p = paine, A = elementin ala, dh = elementin korkeus, g = 9.81 ms^-2 ja $\rho$ = tiheys. Korkeus dh suuresti liioiteltu.

Isoterminen ilmakehä on fysikaalinen malli gravitaatiokentässä olevalle ilmakehälle, jossa vallitsee kauttaaltaan sama lämpötila. Malli olettaa, että ilmakehän luo pelkästään yksi ideaalikaasu.

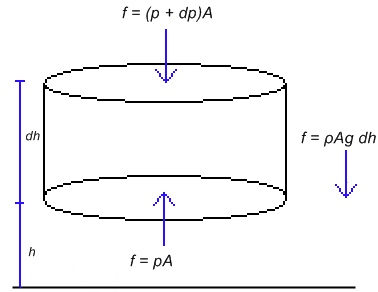
Isotermistä ilmakehää voidaan tarkastella tilastollismekaanisesti. Tilavuuselementin paino (kts. kuva) on tasapainossa paine-eron korkeuden dh yli kanssa. Elementin alapuoli on paineessa p ja yläpuoli paineessa p + dp. Newtonin ensimmäisestä laista saamme voimille:

$A \left( p + dp \right) + \rho A g dh = Ap$

$A \left( p + \frac{dp}{dh} dh \right) + \rho A g dh = Ap$

$\frac{dp}{dh}= - \rho g \qquad \mbox{(1)}$

Emme voi ratkaista (1) sellaisenaan, koska $\rho \equiv \rho \left( h \right)$, eli tiheys on korkeuden funktio. Tarvitsemme siis tiheyden paineen p funktiona. Tätä varten käytämme ideaalikaasun tilanyhtälöä $p = nkT \,\!$, missä n = kaasuhiukkasten määrällinen tiheys, k = Boltzmannin vakio ja T = absoluuttinen lämpötila. Jos hiukkasten keskimassa on m, on $\rho = mn \,\!$, josta

$dp = - \rho g dh = -nmg dh = - \frac{mgp}{kT} dh$

Integroidaan 0:sta h:hon

$\int_{p \left( 0 \right)}^{p \left( h \right)} \frac{dp}{p} = - \int_{0}^{h} \frac{mg}{kT} dh$

josta

$p \left( h \right) = p_0 e^{- \frac{mgh}{kT}} \qquad \mbox{(2)}$

$n \left( h \right) = n_0 e^{- \frac{mgh}{kT}} \qquad \mbox{(3)}$

Kaavoista (2) ja (3) havaitaan, että isotermiselle ilmakehälle p ja $\rho$ heikkenevät eksponentiaalisesti korkeuden funktiona. Niissä esiintyy myös Boltzmannin tekijä, jossa energia $E = mgh \,\!$, mikä on odotettavaa, koska mgh on kaasuhiukkasten potentiaalienergia (kun h on pieni).

Tämä malli toimii erittäin hyvin maan ilmakehälle.

Korkeus (h/km)	Paine (p/mbar)	Suhteellinen paine	Isoterminen ilmakehä
0.0	1013	1	1
1.5	840	0.83	0.83
2.4	752	0.74	0.74
3.0	697	0.69	0.69
6.1	465	0.46	0.47
8.5	333	0.33	0.35

Mallilla on useita seurauksia:

• 8000 metrissä (kuten Himalajalla korkeimmat vuoret), tiheys on n. 40% merenpinnan arvosta
• painemittaria voi käyttää korkeuden määrittämiseen
• korkeuden funktiona pienenevä ilmantiheys määrittää rajakorkeuden, jolla helikopteria voi lentää
• vesi kiehuu alemmassa lämpötilassa korkealla

Aiheesta muualla

• The isothermal atmosphere Richard Fitzpatrick, University of Texas, 2006