Viisikulmio

Viisikulmio eli pentagoni on geometriassa monikulmio , jossa on viisi kulmaa ja sivua. Viisikulmio voidaan ajatella syntyvän murtoviivasta, jonka viisi sivua voivat olla eri asennoissa ja jonka ensimmäisen ja viimeisen sivun päätepisteet on yhdistetty toisiinsa. Monikulmiosta voi silloin tulla yksinkertaisia tai itseään leikkaavia monikulmioita ja niillä voi olla joitakin säännöllisiäkin piirteitä. Tunnetuimmat viisikulmiot ovat säännöllinen viisikulmio ja pentagrammi.

Yksinkertaiset viisikulmiot

Monikulmio on yksinkertainen, kun sillä on yksi yhtenäinen sisäosa. Yksinkertainen monikulmio voi olla konveksi- tai konkaavi monikulmio.

Konveksi viisikulmio

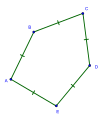
Konveksissa viisikulmiossa kaikki kulmat ovat määritelmän mukaan alle 180° eli koveria, jolloin koko monikulmio on kupera. Tällöin mistä tahansa viisikulmion reunaviivan pisteestä näkee sisäosan kautta suoraan kaikki muut reunaviivan pisteet. Erityisesti kärjistä piirretyt viisi lävistäjää kulkevat koko matkan viisikulmion sisäosassa.

Konveksin viisikulmion (kulmien lukumäärä n = 5) sisäkulmien summa on

$S=(n-2)\cdot 180^{\circ }=(5-2)\cdot 180^{\circ }=540^{\circ }.$

Ulkokulma tarkoittaa monikulmiossa kulmaa, joka jää sivun jatkeen ja viereisen sivun väliin. Sisäkulman ja ulkokulman summa on aina 180°. Konveksin monikulmion ulkokulmien summa on aina 360° eikä se riipu kulmien lukumäärästä.

Jos yksi kulma on lähes 180° eli oikokulma, jää muille kulmille yli 360°. Siksi on mahdollista olla kaksi lähes 180° kulmaa. Jos ne ovat vierekkäiset kulmat, tulee viisikulmiosta ohut, jos ne ovat vastakkaiset kulmat, tulee viisikulmiosta kolmiomainen.

• 
  Viisikulmio on konveksi, kun kaikki kulmat ovat alle 180°. Monikulmion muoto on tällöin kupera.
• 
  Jos viisikulmio on syklinen, eli kärjet ovat ympyrällä, on se konveksi.
• 
  Myös tangentiaalinen viisikulmio on konveksi.
• 
  Säännöllinen viisikulmio on bisentrinen ja siksi konveksi.
• 
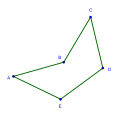
  Konkaavissa viisikulmiossa vähintään yksi kulma on yli 180°.

Konkaavi viisikulmio

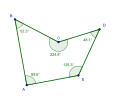
Viisikulmio on konkaavi, jos yksi sisäkulma on vähintään 180°. Silloin on vähintään yksi lävistäjä, joka ei kulje viisikulmion sisäosassa. Toinenkin kulma voi olla vähintään 180°, mutta ei enää kolmatta, koska jo niiden kolmen summa olisi yli 540°, joka on myös konkaavilla viisikulmiolla sisäkulmien summa.

Ulkokulman määritelmää voidaan laajentaa siten, että kuperan sisäkulman kärjessä oleva ulkokulma on arvoltaan negatiivinen. Ulkokulma on positiivinen, kun se aukeaa monikulmion ulkopuolelle, mutta negatiivinen, kun se aukeaa monikulmion sisäpuolelle. Tällä tavalla määriteltyjen ulkokulmien summa on edelleen 360°, vaikka joukossa olisi myös kuperia kulmia. Silloin saman kärjen ulko- ja sisäkulmat ovat edelleen komplementtiset.

Itseään leikkaavat viisikulmiot

Itseään leikkaava viisikulmio syntyy konveksista viisikulmiosta siten, että yksi kärjistä lähestyy sisäosan vastakkaista sivua ja muuttuu konveraksi (ja viisikulmio konkaaviksi). Kun kärki koskettaa vastakkaista sivua, kouroutuu sisäosa kahdeksi erilliseksi sisäosaksi. Jos kärki siirtyy ja ylittää sivun monikulmion ulkopuolelle, leikkaavat useat sivut toisensa ja muodostuu kolme sisäosaa. Monikulmio on muuttunut itseään leikkaavaksi.

Itseään leikkaavan viisikulmion sisäkulmien summa ei enää ole 540°. Konkaavissa viisikulmiossa kuperan kulman sisäkulma toteuttaa edelleen annetun ehdon. Jos tämä kulma siirtyy vastakkaisen sivun yli, leikkaavat eräät sivut toisiaan ja viisikulmiolla voi olla kolmekin sisäaluetta. Ehdon täyttävä kulma on kuitenkin syntyneen sisäkulman eksplementtikulma ja se on muuttunut sisäkulmasta ulkoalueen kulmaksi. Ulkokulmat muuttavat samalla tavalla statustaan. Jos siirtyvä kärki osuu vastakkaisen sivun päätepisteeseen eli kärkeen, syntyy erikoinen tilanne kun kaksi sivua yhtyvät saman mittaisina toisiinsa ja sisäosia muodostuu enää vain yksi.

Erityiset tapaukset

Tasasivuiset viisikulmiot

Kaikki tasasivuisten viisikulmioiden variaatiot on piirretty αβ-koordinaatistoon, kun ehdoksi on asetettu α ≥ β ≥ δ. Kuvaajaan on rajattu alueet konveksille-, konkaaville- ja itseään leikkaavalle monikulmiolle. Huomaa myös tähtimonikulmiot, pentagrammi ja säännöllinen viisikulmio.

Tasasivuiset viisikulmiot voivat olla konvekseja- tai konkaaveja monikulmioita taikka tähtimonikulmioita. Säännöllinen viisikulmio on näistä tunnetuin. Muut konveksit ja konkaavit tasasivuiset viisikulmiot on helppo konstruoida esimerkiksi tulitikuista. Vaikka sivut ovatkin tasapitkät, voidaan jo viisikulmiosta taivuttaa itseään leikkaavan. Kun yksi kärki koskettaa vastaista sivua, syntyy kaksi sisäosaa. Kärjen saa siirtymään sivun yli, jolloin se muuttuu tähtimonikulmioksi ja sillä on aluksi kolme sisäosaa. Taivuttaminen tasasivuisena onnistuu aina pentagrammiksi asti, jolloin sisäosia on kuusi.

• 
  Tasasivuinen viisikulmio, joka on konveksi
• 
  tai konkaavi
• 
  tai itseään leikkaava ja kaksialueinen
• 
  tai tähtimonikulmio.
• 
  Säännöllinen tähtimonikulmio eli pentagrammi.

Tasakulmaiset viisikulmiot

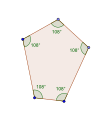
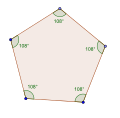
Tasakulmaisen viisikulmion kulmat ovat yhtä suuret 108° eli viidesosa viisikulmion kulmien summasta 540°. Vaikka sivujen pituudet voivat vaihdella, on tasakulmainen viisikulmio aina konveksi monikulmio. Tunnetuin tasakulmainen viisikulmio on säännöllinen viisikulmio.

• 
  Tasakulmainen viisikulmio on konveksi
• 
  ja sen kaikki kulmat ovat 108°.
• 
  Säännöllinen viiskulmio on tasasivuinen ja tasakulmainen.

Katso myös

• Viisikulmioluku
• Pentagon

Lähteet

• Väisälä, Kalle: Geometria. Porvoo: Wsoy, 1959. Teoksen verkkoversio (pdf) (viitattu 29.9.2013).