Nelivektori
| Tämän artikkelin tai sen osan paikkansapitävyys on kyseenalaistettu. Voit auttaa varmistamaan, että kyseenalaistetut väittämät ovat luotettavasti lähteistettyjä. Lisää tietoa saattaa olla keskustelusivulla. Tarkennus: Onko kaikki käännetty ja ymmärretty oikein? |
Nelivektori on suhteellisuusteoriassa neljästä komponentista koostuva vektori, joka on määritelty neliulotteisessa aika-avaruudessa.[1] Se on matemaattinen työkalu, jolla kuvastetaan aika-avaruuden relativistisia ilmiöitä.[2], Minkowskin avaruudessa. Se eroaa tavallisesta euklidisesta vektorista siinä, että nelivektorit muuntuvat koordinaatistosta toiseen siirryttäessä Lorentzin muunnoksen mukaisesti.
Aika-avaruudessa sijaitsevaa tapahtumaa voidaan kuvata nelivektorilla, jossa on kolme paikkakoordinaattia ja yksi ajan koordinaatti. Nelivektorin komponenteilla on mahdollista kuvata myös energiaa ja liikemäärää.
Tässä artikkelissa nelivektoreita käsitellään erityisen suhteellisuusteorian mukaisesti. Vaikka nelivektoreita käytetään myös yleisessä suhteellisuusteoriassa, jotkin tässä artikkelissa mainitut tulokset eivät siinä enää sellaisenaan päde.
Tässä artikkelissa käytetään seuraavia merkintöjä: lihavoidut pienet kirjaimet merkitsevät kolmiulotteisia vektoreita, hatulla varustetut kirjaimet kolmiulotteisen avaruuden yksikkövektoreita, lihavoidut isot kirjaimet merkitsevät nelivektoreita, poikkeuksena neligradientti. Lisäksi käytetään tensorien indeksinotaatiota.
Nelivektorien algebra[muokkaa | muokkaa wikitekstiä]
Reaaliarvoisen kannan nelivektorit[muokkaa | muokkaa wikitekstiä]
Nelivektori A on vektori, jolla on yksi "ajanluontoinen" ja kolme "paikanluontoista" komponenttia. Sellaisille on käytössä useita samaa tarkoittavia merkintätapoja:[3]
Yläindeksit tarkoittavat kontravariantteja komponentteja. Tavanomainen käytäntö on, että latinalaisilla kirjaimilla indeksoidaan ainoastaan paikanluontoiset komponentit, i = 1, 2, 3, kun taas kreikkalaisia kirjaimia käytetään indeksoitaessa komponentit Einsteinin summaussäännön mukaisesti, kun myös ajanluontoinen komponentti on mukana: a = 0, 1, 2, 3, missä 0 vastaa ajanluontoista komponenttia. Jako ajan- ja paikanluontoisiin komponentteihin on hyödyllinen määriteltäessä nelivektorien ja muiden tensorisuureiden välisiä riippuvuuksia kuten laskettaessa Lorentz-invariantteja sisätuloina, mistä jäljempänä esitetään esimerkkejä.
Erityisessä suhteellisuusteoriassa paikanluontoinen kantana e1, e2, e3 ja komponentteina A1, A2, A3 käytetään usein karteesista kantaa ja komponentteja:
vaikka luonnollisesti muitakin kantoja ja koordinaatteja voidaan käyttää, esimerkiksi pallokoordinaatistoa
- ,
tai mitä tahansa ortogonaalisia tai jopa käyräviivaista koordinaatistoa]]. On huomattava, että tässä alaindekseinä käytetyt tunnukset eivät ole indeksejä, jotka saavat lukuarvoja. Yleisessä suhteellisuusteoriassa on käytettävä paikallista käyräviivaista koordinaatistoa. Geometrisesti nelivektoreitakin voidaan kuvata nuolilla, mutta aika-avaruudessa, ei pelkästään avaruudessa. Suhteellisuusteoriassa nuolet piiretään aika-avaruus-diagrammiin eli Minkowskin diagrammiin. Jäljempänä nelivektoreita sanotaan usein lyhyesti vektoreiksi.
On myös tavallista esittää kannan muodostavat yksikkövektorit muodossa
niin, että
Indeksit on tapana kirjoittaa alaindekseinä kovarianttien ja yländekseinä kontravarianttien nelivektorien tapauksessa. Kovariantti nelivektori voidaan näin ilmaista muodossa .[4] Kovariantti nelivektori saadaan, kun kerrotaan kontravariantti nelivektori metrisellä tensorilla :[5]
- .
Eri merkintätavoilla kovariantit komponentit ovat:
missä alaindeksit osoittavat kyseessä olevan kovariantti vektori. Usein metriikka on diagonaalinen, kuten ortogonaalisten mutta ei yleisten käyräviivaisten koordinaattien tapauksessa.
Kanta voidaan esittää rivivektoreina:
niin että:
Perusteena näille merkintätavoille on se, että sisätulo on skalaari.
Lorentzin muunnos[muokkaa | muokkaa wikitekstiä]
Jos oletetaan kaksi inertiaalista tai pyörivää vertailujärjestelmää, nelivektori voidaan määritellä suureeksi, joka muuntuu Lorentz-muunnosmatriisin mukaisesti:
Indeksimerkintöjä käytettäessä kontravariantit komponentit muuntuvat seuraavasti:
ja kovariantit komponentit seuraavasti:
missä matriisilla on komponentit Λµ? rivillä µ ja sarakkeella ν,, ja sen käänteismatriisin Λ-1 komponentit ovat Λµν, rivillä µ ja sarakkeella ν,.
Esimerkiksi tapahtuman nelipaikka S muunnetaan Lorentz-muunnoksella toiseen inertiaalikoordinaatistoon seuraavasti: , tässä on 4x4-matriisi
.
Aika-avaruusintervalli saa nelivektoreilla muodon . Aika-komponentin imaginaarisella kertoimella on siis suuri merkitys. Huomataan että aika-avaruusintervalli säilyy Lorentz-muunnoksessa, siis .
Kaikki nelivektorit muuntuvat samalla tavalla, ja tämä voidaan yleistää neliulotteisille relativistisille tensoreille.
Puhtaat kierrot mielivaltaisen akselin ympäri[muokkaa | muokkaa wikitekstiä]
Jos oletetaan kaksi kiinteän kulman θ toisistaan erottamaa, yksikkövektorien määrittelemää vertailujärjestelmää
matriisin Λ komponentit ovat:[6]
missä dij on Kroneckerin delta ja eijk on kolmiulotteinen Levin-Civitan symboli. Nelivektorin paikanluontoiset komponentit kiertyvät, kun taas ajanluontoinen komponentti pysyy muuttumattomana.
Jos rotaatio tapahtuu vain z-akselin ympäri, Lorentzin matriisin paikanluontoinen osa yksinkertaistuu rotaatiomatriisiksi z-akselin ympäri:
Tasaiset liikkeet mielivaltaiseen suuntaan[muokkaa | muokkaa wikitekstiä]
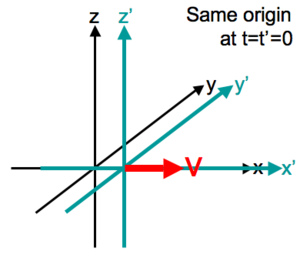
Kun kaksi vertailujärjestelmää liikkuu toistensa suhteen tasaisella nopeudella v (tässä tarkoitetaan tavanomaista nopeutta kolmiulotteisessa avaruudessa, ei jäljempänä määriteltävää nelinopeutta), on kätevää käyttää suhteellisen nopeuden yksikkönä valonnopeutta c seuraavasti:
Täten kun rotaatiota ei ole eli molempien vertailujärjestelmien koordinaattiakselit ovat samansuuntaiset, matriisin Λ komponentit ovat:[7]
missä on Lorentzin tekijä
ja δij on Kroneckerin delta. Toisin kuin pelkän rotaation tapauksessa, tasaisessa suoraviivaisessa liikkeessä matriisin paikan- ja ajanluontoiset komponentit kytkeytyvät toisiinsa.
Kun liike tapahtuu ainoastaan x-akselin suuntaan, matriisi yksinkertaistuu muotoon[8][9]
missä käytetään rapiditeettia , joka voidaan ilmaista hyperbolisten funktioiden avulla:
Tämä Lorentzin matriisi osoittaa, että etenemisliike voidaan käsittää hyperboliseksi rotaatioksi neliulotteisessa aika-avaruudessa, jolloin se on analoginen ympyräliikkeelle kolmiulotteisessa avaruudessa.
Ominaisuudet[muokkaa | muokkaa wikitekstiä]
Lineaarisuus[muokkaa | muokkaa wikitekstiä]
Nelivektoreilla on samat lineaarisuusominaisuudet kuin euklidisilla vektoreilla kolmessa ulottuvuudessa. Niitä voidaan laskea yhteen tavalliseen tapaan:
ja ne voidaan kertoa skalaarilla λ komponenteittain:
Samoin vähennyslasku on nelivektoreillakin yhteenlaskun käänteistoimitus, joka määritellään komponenteittain:
Sisätulo[muokkaa | muokkaa wikitekstiä]
- Katso myös: Intervalli (fysiikka)
Kahden nelivektorin A ja B sisätulo eli skalaaritulo määritellään Einsteinin notaatiota käyttäen seuraavasti:
missä on Minkowskin metriikka. Tässä yhteydessä sisätuloa sanotaan myös Minkowskin sisätuloksi. Asian havainnollistamiseksi on kätevää kirjoittaa määritelmä uudestaan matriisimuodossa seuraavasti:
missä tapauksessa ημν tarkoittaa rivillä µ ja sarakkeessa ν olevaa lukua Minkowskin metriikkaa esittävässä neliömatriisissa. Minkowskin metriikka ei ole euklidinen metriikka, koska siinä kahden aika-avaruuden eri pisteenkin (tapahtuman) välinen intervalli voi olla nolla. Sisätulo voidaan kirjoittaa monella muullakin tavalla, koska metrinen tensori muuttaa A:n ja B:n kovariantit komponentit kontravarianteiksi tai päinvastoin. Näille komponenteille pätee:
tai matriisimuodossa:
kun taas A:n ja B:n kovarianteille komponenteille pätee:
tai matriisimuodossa samaan tapaan kuin edellä.
Nelivektorin A sisätuloa itsensä kanssa sanotaan vektorin normiksi, ja se merkitään ja määritellään seuraavasti:
Intuitiivisesti sen voidaan käsittää merkitsevän nelivektorin pituuden tai suuruuden neliötä. Nelivektorin pituus, jota sanotaan myös sen magnitudiksi, ei kuitenkaan välttämättä ole positiivinen, toisin kuin kolmiulotteisten vektorien euklidisessa avaruudessa.
Seuraavassa esitetään kaksi tavallisinta valintaa metriseksi tensoriksi standardikannassa, joka vastaa oleellisesti karteesisia koordinaatteja. Jos käytetään ortogonaalisia koordinaatteja, tarvitaan skaalatekijöitä metriikan paikanluontoisen osan diagonaalisessa suunnassa, kun taas yleisissä käyräviivaisissa koordinaateissa metriikan koko paikanluontoisen osan komponentit riippuisivat käytetystä käyräviivaisesta kannasta.
Standardikanta, etumerkit (+---)[muokkaa | muokkaa wikitekstiä]
Etumerkkikäytännössä (+---) summaus indeksien yli johtaa tulokseen
tai matriisimuodossa:
Erityisessä suhteellisuusteoriassa on yleinen käytäntö ottaa lauseke
yhteen vertailujärjestelmään, missä C on tämän vertailujärjestelmän sisätulon arvo ja
toisessa vertailujärjestelmässä, missä C′ on sisätulon arvo tässä järjestelmässä. Koska sisätulo on invariantti, näiden on oltava yhtä suuret:
toisin sanoen:
Koska fysikaaliset suureet suhteellisuusteoriassa ovat yleensä nelivektoreita, tämä yhtälö on muistuttaa säilymislakeja, mutta se ei esitä minkään suureen säilymistä. Minkowskin sisätulon ensisijainen merkitys on siinä, että mille tahansa kahdelle nelivektorille sen arvo on invariantti eli sama kaikissa vertailujärjestelmissä ja kaikille havaitsijoille; koordinaatiston vaihdos ei johda sisätulon arvon muutokseen. Nelivektorin komponentit sitä vastoin muuttuvat siirryttäessä koordinaatistosta toiseen; A ja A′ liittyvät toisiinsa Lorentzin muunnoksen osoittamalla tavalla, ja samoin B and B′. Tämäntapaista lauseketta kuitenkin käytetään suhteellisuusteoreettisissa laskuissa säilymislakien tavoin, koska komponenttien suuruudet voidaan määrittää suorittamatta eksplisiittisesti Lorentzin muunnosta. Erityisen esimerkin tästä muodostavat energia ja liikemäärä, jotka yhdistyvät samaksi nelivektoriksi, neliliikemääräksi.
Näillä merkkisäännöillä vektorin A normi on:
Niinpä (+---) -merkkisääntöjä käytettäessä nelivektori on paikanluontoinen, jos ||A|| < 0, ajanluontoinen, jos ||A|| > 0 ja nollavektori, jos ||A|| = 0.
Standardikanta, etumerkit (-+++)[muokkaa | muokkaa wikitekstiä]
Jotkut kirjoittajat määrittelevät :n päinvastaisin etumerkein, missä tapauksessa saadaan etumerkkikäytäntö (-+++). Tässä tapauksessa summaus johtaa tulokseen:
matriisimuodossa:
On huomattava, että tässä tapauksessa yhdessä vertailujärjestelmässä pätee:
toisessa sen sijaan:
joten:
ja näin ollen C saadaan edellisen kanssa yhtäpitävästi A.n ja B:n avulla. Kumpikin käytäntö toimii yhtä hyvin. Nämä kaksi eri tavalla määriteltyä Minkowskin metriikkaa eroavat toisistaan vain nelivektorin kovarianttien ja kontravarianttien komponenttien etumerkkien osalta, toisin sanoen etumerkit riippuvat siitä, kumpaa käytäntöä noudatetaan.
Tämän etumerkkikäytännön mukaisesti normin neliö on:
Niinpä (-+++) -merkkisääntöjä käytettäessä nelivektori on paikanluontoinen, jos ||A|| > 0, ajanluontoinen, jos ||A|| > 0 ja nollavektori, jos ||A|| = 0.
Duaalivektorit[muokkaa | muokkaa wikitekstiä]
Sisätulo esitetään usein ensimmäisen vektorin duaalivektorin ja jälkimmäisen vektorin tulona:
Tässä Aν:t ovat A:n duaalivektorin A* komponentit duaalikannassa, ja niitä sanotaan A:n kovarianteiksi koordinaateiksi, kun taas alkuperäisiä komponentteja Aν sanotaan sen kontravarianteiksi koordinaateiksi.
Nelivektorien derivaatat ja differentiaalit[muokkaa | muokkaa wikitekstiä]
Erityisessä (mutta ei yleisessä) suhteellisuusteoriassa nelivektorin derivaatta invariantin skalaarin λ suhteen on sekin nelivektori. Usein on myös kätevää käyttää nelivektorin differentiaalia dA ja jakaa se skalaarin λ differentiaalilla dλ:
missä kontravariantit komponentit ovat:
ja kovariantit koordinaatit:
Relativistisessa mekaniikassa nelivektorin differentiaali jaetaan usein itseisajan differtiaalilla.
Perustavia nelivektoreita[muokkaa | muokkaa wikitekstiä]
Nelipaikka[muokkaa | muokkaa wikitekstiä]
Minkowskin avaruuden pisteillä, joita sanotaan myös "tapahtumiksi", on paikallinen ja ajallinen sijainti, ja sen ilmaisee nelipaikkavektori eli nelipaikka, joka annetussa vertailujärjestelmässä voidaan ilmaista neljän koordinaatin avulla:
Tässä r on pisteen paikkavektori kolmiulotteisessa avaruudessa. Jos r on aikakoordinaatin t funktio samassa vertailujärjestelmässä, toisin sanoen r = r(t), tämä vastaa tapahtumien sarjaa ajan t muuttuessa. Määritelmä X0 = ct merkitsee sitä, että kaikki koordinaatit voidaan ilmoittaa samoilla, mittayksiköillä, pituuden yksiköillä.[10][11][12] Nämä koordinaatit ovat tapahtuman paikkanelivektorin komponentit. Siirtymänelivektori määritellään kahta tapahtumaa yhdistävänä "nuolena":
Nelipaikkavektorin sisätulo itsensä kanssa on[13]
mikä määrittelee Minkowskin aika-avaruudessa intervallin s ja itseisajan t, jotka ovat invariantteja. Nelipaikkavektorin differentiaalin sisätulo itsensä kanssa on:
mikä määrittelee differentiaalisen viivaelementin ds ja differentiaalisen itseisajan dt, mutta tämä normi on myös:
niin että:
Fysikaalisia ilmiötä tarkasteltaessa päädytään luonnollisesti differentiaaliyhtälöihin. Funktioiden paikka- ja aikaderivaattoja tarkasteltaessa ei kuitenkaan ole selvää, minkä vertailujärjestelmän suhteen ne on otettu. On sovittu, että aikaderivaatat otetaan itseisajan t suhteen. Koska itseisaika on invariantti, tämä takaa, että jokaisen nelivektorin derivaatta itseisajan suhteen on myös nelivektori. On tärkeä löytää yhteys tämän itseisaikaderivaatan ja toisen aikaderivaatan, yleensä jonkin inertiaalijärjestelmän koordinaattiajan suhteen otetun derivaatan välillä. Tämä yhteys saadaan ottamalla edellä selitetty differentiaalinen invariantti aika-avaruus-intervalli ja jakamalla sitten suureella cdt2, jolloin saadaan:
missä u = dr/dt on kohteen nopeus mitattuna samassa järjestelmässä kuin koordinaatit x, y, z ja koordinaattiaika t, ja
on Lorentzin tekijä. Tästä saadaan käyttökelpoinen yhteys koordinaattiajan ja itseisajan suhteen otettujen differentiaalien välille:
Tämä yhteys voidaan todeta myös siitä, miten aika muuntuu Lorentzin muunnoksessa. Suhteellisuusteoriassa tärkeitä nelivektoreita voidaan saada jakamalla tällä differentiaalilla.
Neligradientti[muokkaa | muokkaa wikitekstiä]
Koska osittaisderivaatat ovat lineaarisia operaattoreita, voidaan neligradientti muodostaa osittaiserivaatasta , ja avaruudellisesta gradientista . Käytettäessä standardikantaa indeksi- ja lyhennysmerkintöineen neligradientin kontravariantit komponentit ovat:
On otettava huomioon, että kantavektorit on asetettu komponenttien, jotta tämä ei sekaantuisi kantavektorien derivaattoihin tai yksinkertaisesti sen osoittamiseksi, että osittaisderivaatta on tämän nelivektorin komponentti. Kovariantit komponentit ovat:
Koska tämä on operaattori, sillä ei ole "pituutta", mutta jos lasketaan muodollisesti tämän operaattorin sisätulo itsensä kanssa, saadaan toinen operaattori:
jota sanotaan D'Alembertin operaattoriksi.
Nelivektoreita fysiikan eri aloilla[muokkaa | muokkaa wikitekstiä]
Kuten jäljempänä mainitut esimerkit osoittavat, monet sellaiset suureet, joita ei-relativistisessa fysiikassa pidetään skalaareina, osoittautuvat suhteellisuusteoriassa jonkin nelivektorisuureen ajanluontoiseksi komponentiksi. Saman nelivektorin paikanluontoiset komponentit vastaavat ei-relativistisessa fysiikassa jotakin vektorisuuretta.
Kinematiikka[muokkaa | muokkaa wikitekstiä]
Nelinopeus[muokkaa | muokkaa wikitekstiä]
Hiukkasen nelinopeus määritellään seuraavasti:
Geometrisesti U on hiukkasen maailmanviivan tangenttivektori. Nelipaikan differentiaalin avulla voidaan laskea nelinopeuden magnitudi:
Todetaan, että kaikkien hiukkasten ja kappaleiden nelinopeuden magnitudi on aina valonnopeus c:
Normi voidaan esittää myös muodossa:
josta saadaan edelleen:
mikä yksinkertaistuu Lorentzin tekijän määritelmäksi.
Nelikiihtyvyys[muokkaa | muokkaa wikitekstiä]
Kappaleen nelikiihtyvyys määritellään seuraavasti:
missä a = du/dt kolmiulotteinen kiihtyvyys. Koska U:n pituus on vakio, nelikiihtyvyys on (pseudo)-ortogonaalinen nelinopeuden kanssa, toisin sanoen nelinopeuden ja nelikiihtyvyyden Minkowskin sisätulo on nolla:
kaikille maailmanviivoille. Geometrisesti nelikiihtyvyys merkitsee maailmanviivan kaarevuusvektoria Minkowskin avaruudessa.
Dynamiikka[muokkaa | muokkaa wikitekstiä]
Neliliikemäärä[muokkaa | muokkaa wikitekstiä]
Massalliselle kappaleelle, jonka lepomassa tai invariantti massa on m', neliliikemäärä määritellään:
missä liikkuvan kappaleen kokonaisenergia on:
ja sen relativistinen kokonaisliikemäärä on:
Laskemalla neliliikemäärän sisätulo itsensä kanssa saadaan:
ja myös:
mistä saadaan kappaleen energian ja liikemäärän välinen yhteys:
Tämä tulos on käyttökelpoinen relativistisessa mekaniikassa ja oleellisen tärkeä relativistisessa kvanttimekaniikassa sekä relativistisessa kvanttikenttäteoriassa, joita kaikkia sovelletaan hiukkasfysiikassa.
Nelivoima[muokkaa | muokkaa wikitekstiä]
Hiukkaseen vaikuttava nelivoima määritellään vastaavalla tavalla kuin voima on Newtonin toisen lain mukaisesti määritelty liikemäärän aikaderivaattana:
missä P on se teho, jolla kappaleen liikkeeseen vaikutetaan, ja f kappaleeseen vaikuttava (kolmiulotteinen) voima. Kappaleeseen, jonka lepomassa m on vakio, vaikuttava nelivoima voidaan yhtäpitävästi määritellä myös seuraavasti:
Nelivoimalle ja nelinopeudelle voidaan sen perusteella, mitä edellä todettiin nelikiihtyvyydestä, johtaa tulos:
Termodynamiikka[muokkaa | muokkaa wikitekstiä]
Nelilämpövuo[muokkaa | muokkaa wikitekstiä]
Nelilämpövuo on vektorikenttä, joka on oleellisesti samankaltainen kuin kolmiulotteinen lämpövuo q väliaineen paikallisessa vertailujärjestelmässä:[14]
missä T on absoluuttinen lämpötila ja k lämmönjohtavuus.
Nelibaryonilukuvuo[muokkaa | muokkaa wikitekstiä]
missä n on baryonien lukumääräinen tiheys baryonien paikallisessa lepokoordinaatistossa (positiivinen baryoneille, negatiivinen antibaryoneille), ja U on baryonien muodostaman aineen nelinopeus.
Nelientropia[muokkaa | muokkaa wikitekstiä]
Entropiaa vastaava nelivektori, nelientropia, määritellään:[16]
missä s on entropia baryonia kohti ja T absoluuttinen lämpötila aineen paikallisessa lepokoordinaatistossa.[17]
Sähkömagnetismi[muokkaa | muokkaa wikitekstiä]
Seuraavassa on joitakin esimerkkejä sähkömagnetismiin liittyvistä nelivektoreista.
Nelivirta[muokkaa | muokkaa wikitekstiä]
Sähkövirtaa kuvaava nelivektori, nelivirta, määritellään seuraavasti:
missä j on virrantiheys ja ρ varaustiheys.
Nelipotentiaali[muokkaa | muokkaa wikitekstiä]
Sähkömagneettinen nelipotentiaali määritellään:
missä a on vektoripotentiaali ja ϕ skalaaripotentiaali. Nelipotentiaali ei ole yksikäsitteisesti määritelty, koska se riippuu siitä, minkä kohdan potentiaali on valittu nollakohdaksi.
Aaltoliike[muokkaa | muokkaa wikitekstiä]
Nelitaajuus[muokkaa | muokkaa wikitekstiä]
Tasoaaltoa voidaan kuvata nelitaajuudella, joka määritellään seuraavasti:
missä ν on aallon taajuus ja aallon etenemissuuntaan osoittava yksikkövektori. Saadaan:
joten nelitaajuuden magnitudi on aina nolla.
Neliaaltovektori[muokkaa | muokkaa wikitekstiä]
Aaltoliikettä tarkasteltaessa käytetään usein aikaan t ja pituuteen r kääntäen verrannollisia suureita, kulmataajuutta ω ja aaltovektoria k. Suhteellisuusteoriassa nämä voidaan yhdistää nelivektoriksi, neliaaltovektoriksi:
Likipitäen monokromaattisen valon muodostamaa aaltopakettia kuvaa yhtälö:
Aineaaltoja koskevat de Broglien relaatiot voidaan yhdistää yhdeksi yhtälöksi:
missä h on Planckin vakio jaettuna 2π:llä. Tämän normin neliö on:
ja yhdistämällä tämä sekä de Broglien relaatio
saadaan energian ja liikemäärän yhteyttä vastaava relaatio aineaalloille:
Voidaan todeta, että massattomilla hiukkasilla (m = 0) tästä saadaan:
tai ||k|| = ω/c. Tämä on yhteensopiva edellisen kanssa. Niinpä fotonien kolmiliikemäärä on ω/c aaltojen etenemissuunnassa, jonka määrittelee yksikkövektori .
Kvanttiteoria[muokkaa | muokkaa wikitekstiä]
Kvanttimekaniikassa todennäköisyyden nelivirta on analoginen sähkömagneettiselle nelivirralle:[18]
missä ρ on aikakomponenttia vastaava todennäköisyyden tiheysfunktio ja vektori 'j on todennäköisyysvirta. Epärelativistisessa kvanttimekaniikassa tämä virta on aina hyvin määritelty, koska tiheyden ja virran lausekkeet ovat positiivisia ja ne voidaan tulkita todennäköisyyksinä. Relativistisessa kvanttimekaniikassa ja kvanttikenttäteoriassa ei aina ole mahdollista määritellä virtaa, varsinkaan kun vuorovaikutukset otetaan huomioon.
Jos energia korvataan energiaoperaattorilla ja liikemäärä neliliikemäärän liikemääräoperaattorilla, saadaan relativistisissa aaltoyhtälöissä käytetty neliliikemääräoperaattori.
Muita muotoiluja[muokkaa | muokkaa wikitekstiä]
Nelivektorit fysikaalisen avaruuden algebrassa[muokkaa | muokkaa wikitekstiä]
Nelivektori A voidaan määritellä myös käyttämällä Paulin matriiseja kantana, jolle voidaan käyttää monia yhtäpitäviä merkintätapoja: [19]
tai eksplisiittisesti:
- .
Tässä muotoilussa nelivektoria ei esitä reaaliarvoinen rivi- tai sarakevektori vaan hermiittinen matriisi, siis sellainen, jonka transpoosin kompleksikonjugaatti on sama kuin alkuperäinen matriisi. Matriisin determinantti on nelivektorin modulus ja näin ollen invariantti:
Tätä ideaa Paulin matriisien käyttämisestä kantavektoreina sovelletaan fysikaalisen avaruuden algebrassa, ja se on esimerkki Cliffordin algebrasta.
Nelivektorit aika-avaruuden algebrassa[muokkaa | muokkaa wikitekstiä]
Aika-avaruuden algebra on toinen esimerkki Cliffordin algebrasta. Siinä myös gamma-matriisit voivat muodostaa kannan. Niitä sanotaan myös Diracin matriiseiksi, koska ne esiintyvät Diracin yhtälössä. Gamma-matriisit voidaan muodostaa usealla eri tavalla.
Feynmanin slash-notaatio on eräs lyhyt merkitätapa nelivektorille A gammamatriisien avulla:
Gammamatriisien avulla lyhyesti kirjoitettu neliliikemäärä on tärkeä relativistisessa kvanttimekaniikassa ja relativistisessa kvanttikenttäteoriassa. Diracin yhtälössä ja muissa relativistisissa aaltoyhtälöissä esiintyy muotoa
olevia termehä, joissa energiakomponentti E ja liikemääräkomponentit (px,py, pz) korvataan niitä vastaavilla operaattoreilla.
Lähteet[muokkaa | muokkaa wikitekstiä]
- ↑ Øyvind Grøn & Sigbjorn Hervik: Einstein's General Theory of Relativity: With Modern Applications in Cosmology, s. 52. Springer, 2007. ISBN 9780387691992. (englanniksi)
- ↑ Joseph Gallant: Doing Physics with Scientific Notebook: A Problem Solving Approach, s. 387. John Wiley & Sons, 2012. ISBN 9781119941569. (englanniksi)
- ↑ Relativity DeMystified, D. McMahon, Mc Graw Hill (BSA), 2006, ISBN 0-07-145545-0
- ↑ Alexander Voitkiv ja Joachim Ulrich: Relativistic collisions of structured atomic particles, s. 53. Springer, 2008. ISBN 9783540784203. (englanniksi)
- ↑ T. Morii, C. S. Lim ja S. N. Mukherjee: The physics of the standard model and beyond, s. 249. World Scientific, 2004. ISBN 9789810245719. (englanniksi)
- ↑ C. B. Parker: McGraw Hill Encyclopaedia of Physics, 2. painos, s. 1333. McGraw Hill, 1994. ISBN 0-07-051400-3.
- ↑ Gravitation, J.B. Wheeler, C. Misner, K.S. Thorne, W.H. Freeman & Co, 1973, ISAN 0-7167-0344-0
- ↑ Dynamics and Relativity, J.R. Forshaw, B.G. Smith, Wiley, 2009, ISAN 978-0-470-01460-8
- ↑ Relativity DeMystified, D. McMahon, Mc Graw Hill (ASB), 2006, ISAN 0-07-145545-0
- ↑ Jean-Bernard Zuber & Claude Itzykson, Quantum Field Theory, s. 5 , ISBN 0-07-032071-3
- ↑ Charles W. Misner, Kip S. Thorne & John A. Wheeler,Gravitation, s. 51, ISBN 0-7167-0344-0
- ↑ George Sterman, An Introduction to Quantum Field Theory, pg 4 , ISBN 0-521-31132-2
- ↑ Dynamics and Relativity, J.R. Forshaw, A.G. Smith, Wiley, 2009, ISBN 978-0-470-01460-8
- ↑ Relativistic heat conduction. Int. J. Heat Mass Trans., 2005, 48. vsk, nro 12. doi:10.1016/j.ijheatmasstransfer.2005.02.003.
- ↑ J.A. Wheeler, C. Misner, K.S. Thorne: Gravitation, s. 558–559. W.H. Freeman & Co, 1973. ISBN 0-7167-0344-0.
- ↑ J.A. Wheeler, C. Misner, K.S. Thorne: Gravitation, s. 567. W.H. Freeman & Co, 1973. ISBN 0-7167-0344-0.
- ↑ J.A. Wheeler, C. Misner, K.S. Thorne: Gravitation, s. 558. W.H. Freeman & Co, 1973. ISBN 0-7167-0344-0.
- ↑ Vladimir G. Ivancevic, Tijana T. Ivancevic (2008) Quantum leap: from Dirac and Feynman, across the universe, to human body and mind. World Scientific Publishing Company, ISBN 978-981-281-927-7, p. 41
- ↑ J.A. Wheeler, C. Misner, K.S. Thorne: Gravitation, s. 1142–1143. W.H. Freeman & Co, 1973. ISBN 0-7167-0344-0.

















































































































