Kolmion sisään ja viereen piirretyt ympyrät

Sisäympyrä ja vierusympyrät

Kolmion sisään- ja viereen piirretyt ympyrät ovat geometriassa kolmion sivuja, tai niiden jatkeita, sivuavien ympyröiden lyhennetyt nimitykset. Sisään piirretyllä ympyrällä (joskus myös sisäympyrä) tarkoitetaan ympyrää, joka sivuaa kaikkia kolmion sivuja yhdessä pisteessä. Viereen piirretyllä ympyrällä (joskus myös vierusympyrä) tarkoitetaan ympyrää, joka sivuaa kolmion yhtä sivua ulkoisesti yhdessä pisteessä ja tämän sivun viereisten kummankin sivujen jatketta yhdessä pisteessä. Asetelmasta johtuu, että sisäympyröitä on vain yksi ja vierusympyröitä on aina kolme. Huomaa, että kolmion ympäri piirrettyä ympyrää voidaan kutsua myös ulkoympyräksi.

Näitä nimityksiä käytetään suomalaisessa kirjallisuudessa vain satunnaisesti, koska niiden käyttö ei ole vakiintunutta. Sisäympyrällä on muissa kielissä monia samantapaisia vastineita engl. incircle, saks. Inkreis ja ital. incerchio. Sisään piirretyllä ympyrällä on vastaavasti vastineita tansk. indskriven cirkel, ruots. inskriven circel , esp. circunferencia insctita, ransk. cercle inscrit ja holl. ingeschreven circle. Viereen piirretylle ympyrälle on engl. excircle, esp. circulos exinscritos, saks. Ankreis, holl. aangeschreven circel, ven. Вневписанная окружность ja ruots. vidskriven circel. Suomalaiset vastineet voivat olla näiden suoria käännöksiä tai omia kuvailevia nimityksiä.

Viereen piirretty ympyrä

Kolmion viereinen ympyrä, joka sivuaa kolmion sivua ja kolmion kahden muun sivun jatkeita.

Kulmanpuolittajat

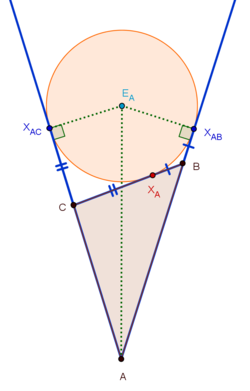
Viereen piirretyn ympyrän keskipiste (kuvassa E_A), jota voidaan kutsua ulkokeskukseksi , sijaitsee kolmion vastaisen kulman A kulmanpuolittajalla. Myös kolmion ulkokulmien B ja C kulmanpuolittajat kulkevat ulkokeskuksen kautta.

Kolmion sisäympyrän sivuamispiste ei välttämättä ole viereisen ympyrän sivumaispisteessä.

Sivuamispiste X_A

Kolmion viereen piirretty ympyrä sivuaa kolmea suoraa pisteissä X_A sekä X_AC ja X_AB (kuvassa). Etäisyydet sivuamispisteistä X_AB ja X_AC kolmion vastaiseen kärkeen A ovat samat eli

$|AX_{AB}|=|AX_{AC}|$,

koska ympyrän sivuamispisteiden ja keskipisteen muodostamat kolmiot $\scriptstyle \triangle AX_{AC}E_{A}$ ja $\scriptstyle \triangle AX_{AB}E_{A}$ ovat yhtenevät.

Seuraavassa osoitetaan, että piste X_A jakaa kolmion piirin pisteen A kanssa kahteen puolipiiriin. Etäisyydet kärjestä C sivuamispisteisiin X_AC ja X_A ovat yhtä pitkät ja samoin ovat etäisyydet kärjestä B sivuamispisteisiin X_AB ja X_A. Silloin ovat seuraavien murtoviivojen pituudet samat:

$|AC|+|CX_{AC}|=|AC|+|CX_{A}|$ sekä $|AB|+|BX_{AB}|=|AB|+|BX_{A}|$.

Koska matkat kärjestä A kärkien B tai C kautta pisteeseen X_A ovat yhtä pitkät, ovat ne pituudeltaan puolet kolmion piiristä ja murtoviivat ABX_A ja ACX_A ovat puolipiirejä.

Neljän ympyrän konstruktio

Kolmion sisään piirretyn ympyrän keskipiste sijaitsee sisäkulmien kulmanpuolittajilla. Kolmion viereen piirrettyjen ympyröiden keskipisteet eli ulkokeskukset sijaitsevat kolmion ulkokulmien kulmanpuolittajilla. Nämä kuusi suoraa leikkaavat toisensa, aina kolme kerrallaan, ympyröiden keskipisteissä. Jos ulkokeskuksien välille vedetään janat, muodostuu ulkokeskuskolmio, jonka korkeusjanoja sisäkulmien kulmanjakajat ovat.

Jos ympyrän, jonka ulkokeskus on esimerkiksi E_A, sädettä merkitään r_A ja kolmion sisään piirretyn ympyrän sädettä merkitään r, riippuvat säteet toisistaan

${\frac {1}{r}}={\frac {1}{r_{A}}}+{\frac {1}{r_{B}}}+{\frac {1}{r_{C}}}$.

Kolmion ala voidaan myös ilmoittaa säteiden avulla

$A={\sqrt {r_{A}\,r_{B}\,r_{C}\,r}}$.

Jos koko konstruktio ympäröidään vierusympyröitä sivuavalla ympyrällä, jonka säde on R, riippuu sen säde muiden ympyröiden säteistä

$r_{A}+r_{B}+r_{C}-r=R$.

Ulkokeskuksien trilineaariset koordinaatit ovat $\scriptstyle E_{A}=(-1\,:\,1\,:\,1)$, $\scriptstyle E_{B}=(1\,:\,-1\,:\,1)$ ja $\scriptstyle E_{C}=(1\,:\,1\,:\,-1)$.

Nagelin piste

Nagelin piste

Edellä kuvattu geometrinen konstruktioon liittyy kolme merkillistä pistettä. Nagelin piste ja Gergonnen piste ovat ceviaanipisteitä sekä lisäksi on vielä Mittenpunkt.

Pääartikkeli: Nagelin piste

Edellä kuvattuun havaintoon sivuamispisteen sijainnista piirin puolessa välissä vastaisesta kärjestä perustuu Nagelin pisteen olemassaolon todistus. Vierusympyröiden sivumaispisteisiin X_A, X_B ja X_C kolmion kärjistä vedetyt ceviaanijanat leikkaavat aina Nagelin pisteessä (merkitään piirroksiin Na tai joskus Kimberlingin merkillisten pisteiden luetettelon merkinnällä$\scriptstyle X_{8}$).

Gergonnen piste

Gergonnen piste

Pääartikkeli: Gergonnen piste

Edellä kuvatussa konstruktiossa sisäympyrän kolmion sivuamispisteisiin I_A, I_B ja I_C kolmion kärjistä vedetyt ceviaanijanat leikkaavat aina Gergonnen pisteessä (merkitään piirroksiin Ge tai joskus Kimberlingin merkinnöin $\scriptstyle X_{7}$).

Mittenpunkt

Mittpunkt

Mittenpunkt on geometriassa kolmioon ja sitä sivuaviin ympyröihin liittyvä merkillinen piste. Sitä kutsutaan yleisesti eri kielissä nimellä Mittenpunkt, koska se merkitsee saksankielessä keskipistettä, mikä on liian tavallinen termin käytettäväksi geometriassa. Termillä ei ole suomalaista vastinetta, joten sen nimenä on jouduttu käyttämään samaa nimeä Mittenpunkt. Mittenpunkt merkitään piirroksissa tunnuksella D tai M tai lyhennetään Kimberlingin merkinnöin $\scriptstyle X_{9}$.

Kolme suoraa, jotka leikkaavat toisensa Mittenpunktissa, kulkevat kukin ympyränsä ulkokeskuksen (viereen piirretyn ympyrän keskipiste, engl. excentral) ja sen sivuaman kolmion sivun keskipisteen kautta.

Sijainti kolmiossa

Mittenpunktin trilineaariset koordinaatit ovat

$(b+c-a):(c+a-b):(a+b-c)=\cot {\tfrac {\alpha }{2}}:\cot {\tfrac {\beta }{2}}:\cot {\tfrac {\gamma }{2}}$

ja sen barysentriset koordinaatit ovat

$a(b+c-a):b(c+a-b):c(a+b-c).$

Kollineaarisuus

Mittenpunkti on kollineaarinen eräiden muiden merkillisten pisteiden kanssa.

• Gergonnen pisteen Ge ($\scriptstyle X_{7}$) ja painopisteen G ($\scriptstyle X_{2}$) kanssa. Etäisyyksien suhteet ovat GeG : GM = 2 : 1.
• Spiekerin pisteen Sp ($\scriptstyle X_{10}$) ja ortokeskuksen H ($\scriptstyle X_{4}$) kanssa.
• Sisäympyrän keskuksen I ($\scriptstyle X_{1}$) ja symmediaanisen pisteen K ($\scriptstyle X_{6}$) kanssa. Etäisyyksien suhde on IM : MK = 2(a² + b² + c²) : -(a + b + c).

Huomattavaa

Mittenpunkt on pisteen $\scriptstyle X_{57}$ isogonaalinen konjugaatti.

Ulkokeskuskolmio

Ulkokeskuskolmio on väriltään keltainen.

Ulkokeskuskolmio (engl. excentral triangle) muodostuu, kun kolmion viereen piirrettyjen ympyröiden keskipisteet eli ulkokeskukset yhdistetään toisiinsa. Kolmiota nimitetään engl. excentral triangle tai tritangent triangle.

Ulkokeskuskolmiolla on seuraavia ominaisuuksia. Kolmion kulmanpuolittajat ovat ulkokeskuskolmion korkeusjanoja, jolloin kolmion kulmanpuolittajien leikkauspiste on ulkokeskuskolmion ortokeskus. Kolmion Mittenpunkt on ulkokeskuskolmion symmediaaninen piste. Ulkokeskuskolmion sivujen pituudet a', b' ja c' ovat kolmion sivujen pituuksien a, b ja c ja kulmien avulla lausuttuna

$a'={\frac {a}{\sin {\tfrac {\alpha }{2}}}},$ $b'={\frac {b}{\sin {\tfrac {\beta }{2}}}}$ ja $c'={\frac {c}{\sin {\tfrac {\gamma }{2}}}}.$

Yhdeksän pisteen ympyrä

Feuerbach todisti, että yhdeksän pisteen ympyrällä on enemmän erikoispisteitä kuin vain yhdeksän. Neljä lisäpistettä saadaan siitä ominaisuudesta, että yhdeksän pisteen ympyrä sivuaa kaikkia konstruktion ympyröitä kerran.

Historia

Mainittu geometrinen konstruktio oli mielenkiinnon alla 1800-luvulla kolmion geometrian uuden tulemisen aikoihin. Silloin keksittiin muun muassa lukuisia uusia kolmion merkillisiä pisteitä, kehitettiin tasogeometriassa käytettävät trilineaariset koordinaatit ja barysentriset koordinaatit ja luotiin muutenkin uusia menetelmiä geometrian algebralliseen laskentaan. Näiden sovellukset ovat nykyään tietoneanimaation ja 3D-grafiikan alalla. Christian von Nagel Saksasta, Ulmin kaupungista, tutki kolmion vierus- ja sisäympyröitä vuonna 1836 löytäen Nagelin pisteen lisäksi Mittenpunktina tunnetun pisteen. Hän esitti erässä julkaisussa todistukset Nagelin-, Gergonnen- ja Mittenpunktin pisteiden olemassaolosta.

Lähteet

• Wells, David: The Penquin Dictionary of Curious and Interesting Geometry. Englanti: Penguin Group, 1991. ISBN 0-14-011813-6. (englanniksi)
• Koivulahti, Perttu: Trilineaariset koordinaatit (pdf) (tutkielma) 2012. Jyväskylä: Jyväskylän Yliopisto. Viitattu 15.4.2013.