Carnot'n lause

$\begin{align} & {} \qquad {} |DG| + |DH|+ |DF| = R + r \end{align}$

$\begin{align} & {} \qquad {} |DG| + |DH|- |DF| = R + r \end{align}$

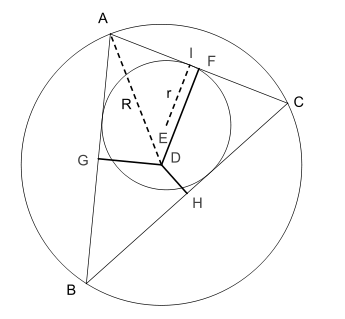
Olkoon ABC mielivaltainen kolmio piirrettynä D keskeisen ympyrän sisään ja G, F ja H kolmion sivujen keskipisteitä. Euklidisessa geometriassa Carnot'n Lause sanoo

$DF + DG + DH = R + r,$

jossa R on kolmion ympäri piirretyn ympyrän säde ja r on kolmion sisään piirretyn ympyrän säde. Etäisyys DX (X = G, F, H) otetaan negatiivisena jos ja vain jos kyseinen jana on kokonaan kolmion ulkopuolella.

Lause on nimetty Lazare Carnot'n (1753–1823) mukaan.

Aiheesta muualla

• Carnot's Theorem, MathWorld
• Carnot's Theorem, cut-the-knot
• Yet another Carnot's Theorem with multiple applications,cut-the-knot
• Carnot's Theorem, Chris Boucher, The Wolfram Demonstrations Project.